植物为何钟爱数学,数学家为何痴迷植物
观察植物世界,你会发现叶片、茎干和根系的形态与排列中,藏着许多美丽而迷人的结构。有些简洁对称,有些以优雅的斐波那契螺旋排布,还有些呈现出分形般的图案。这些结构为何能形成得如此规整且具有可重复性?正如本讲座所揭示的,这类排列往往遵循着简单的规律,而这些规律我们完全可以通过数学来透彻理解。

图源:gresham.ac.uk
作者:阿兰・戈里利(Alain Goriely)格雷沙姆几何学教授 2025-11-11
译者:zzllrr小乐(数学科普公众号)2026-1-10

接上一章格雷沙姆讲座系列之《自然几何与万物形态》第1章:手的形态——对称性、手性与旋向性——Alain Goriely教授
第2章:植物的形态 —— 植物为何钟爱数学,数学家为何痴迷植物
我们将继续通过数学的视角探索自然界。很快我们就会发现,一片格外丰富的数学领域,就自然生长在我们的后花园中。植物、花朵和树木美不胜收,为我们的心灵带来无尽喜悦与宁静。这种美感的一部分,源于植物各器官的规律性、多样性及其非凡的形态。事实上,茎、种子和花瓣的形态与排列方式,一直是数学家们长期研究的课题 —— 它们遵循着异常简洁的规律。
2.1 植物钟爱数学
有些植物展现出非凡的秩序感。当我们仔细观察它们的叶片和花朵时,会发现一种近乎神奇的规律性与对称性。例如,花瓣的排列往往暗含着精妙的精准度:毛茛有 5 片花瓣,百合有 6 片,雏菊有 10 片或 21 片,这种排列方式天然契合我们的审美感知(更多示例见下方)。

Stapelia gigantea:巨花犀角、大犀角(萝藦科犀角属多肉植物,俗称 “海星花”)

Stapelia flavopupurea:黄花犀角(萝藦科犀角属,“flavo-” 为拉丁语 “黄色”,“popupurea” 指 “紫色晕染”,因花朵常带黄紫相间色彩得名)

Parodia magnifica:壮丽仙人球(仙人掌科锦绣玉属,“magnifica” 意为 “壮丽的”,形容其球体与花型美观)
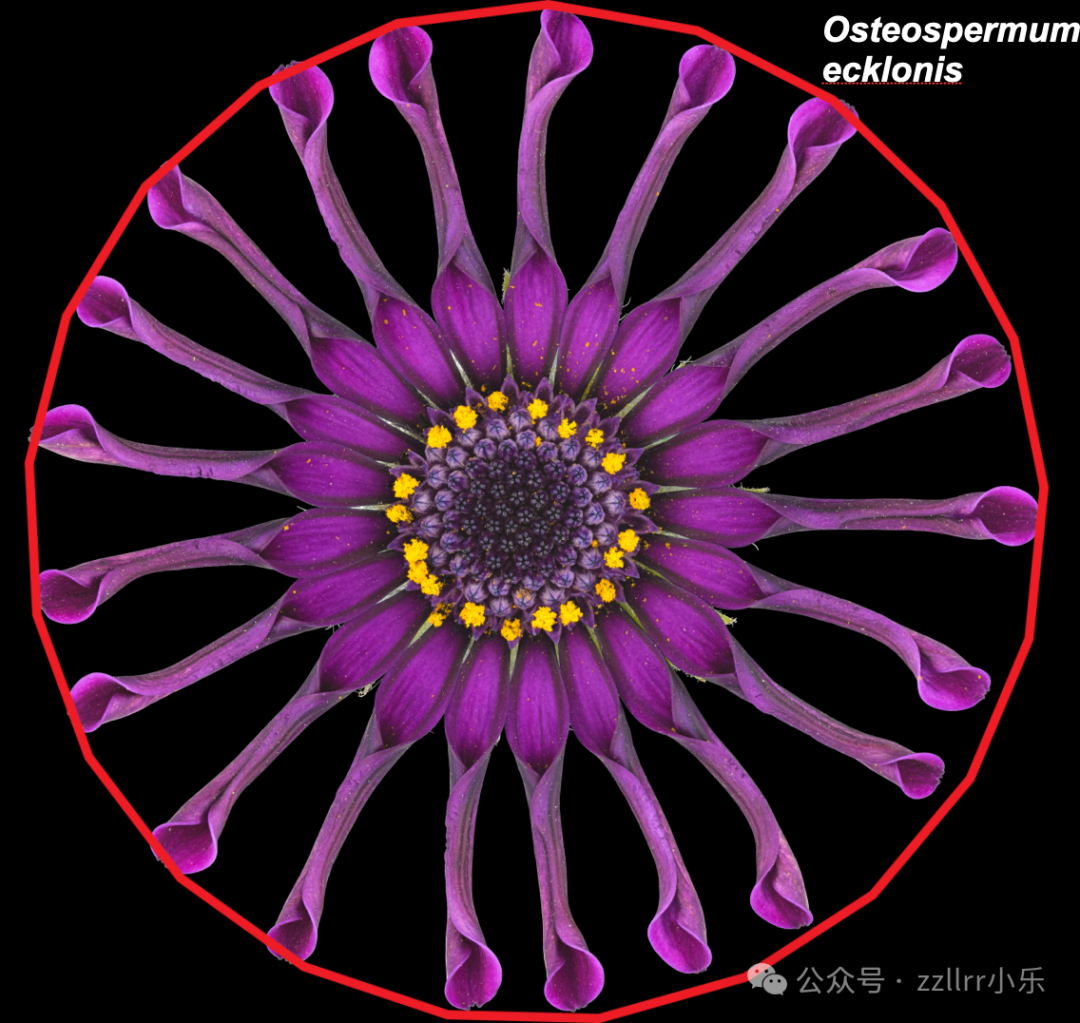
Osteospermum ecklonis:蓝眼菊(菊科蓝眼菊属,常见园艺花卉,“ecklonis” 为纪念植物学家 Christian Friedrich Ecklon 而命名)
图 2.1:植物中的规律性
随意观察花朵和植物,就能发现不同的对称类型。
照片由Victor Mozqueda提供(见致谢部分)
许多植物的另一个典型特征是螺旋结构的存在。螺旋无处不在:种子、花瓣和小花的排列中,蕨类叶片的舒展过程中,攀缘藤蔓的旋转缠绕中,都能见到它的身影。一旦开始留意,你会发现它遍布各处。但最令人惊叹、最引人注目的几何特征,出现在罗马花椰菜上 —— 它的表面由螺旋状的圆锥体构成,这些圆锥体在越来越小的尺度上相互呼应。每个小花球都是整个花椰菜的完美微缩版,呈现出多重层级,形成了一件鲜活的分形雕塑,其塑造者正是多尺度下自我相似生长这一简单行为(见图2.3)。
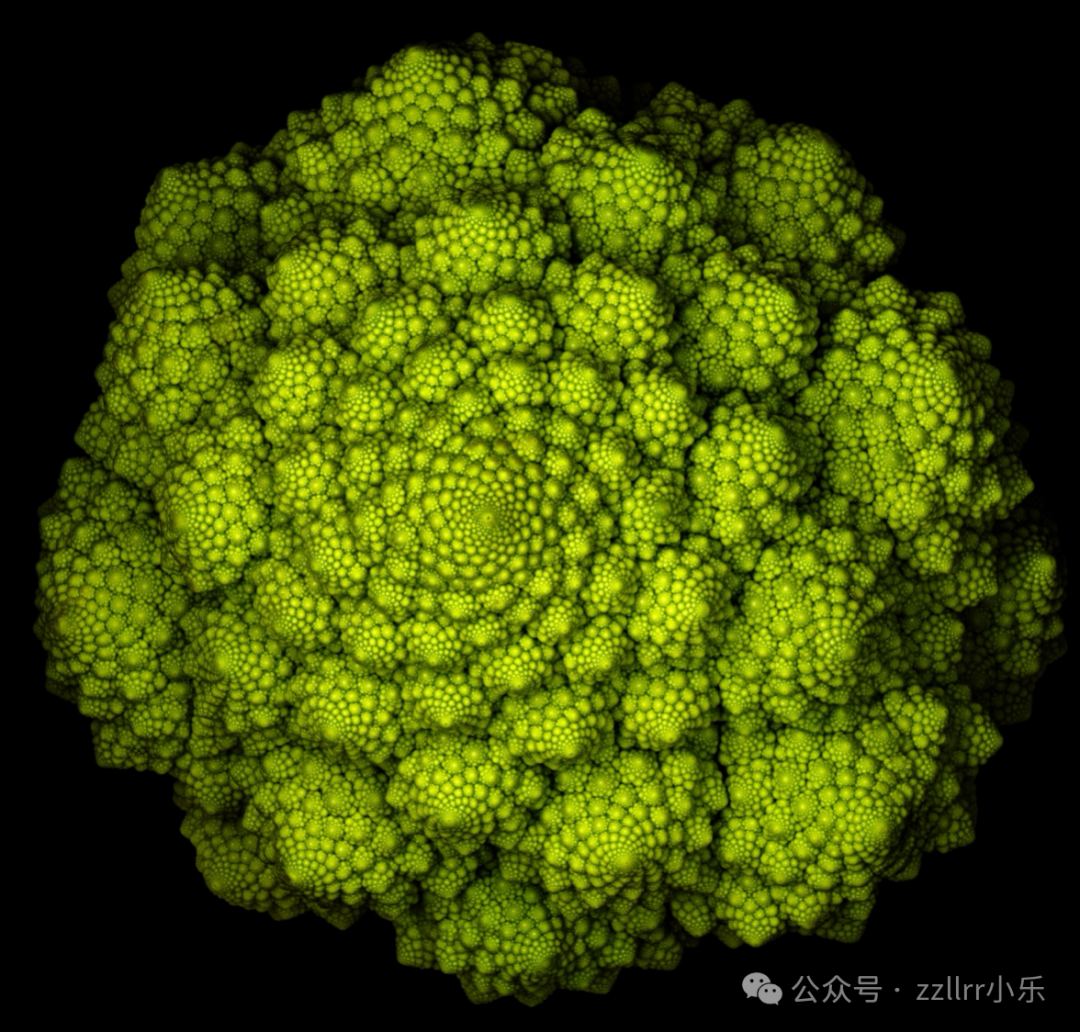
图 2.3:罗马花椰菜
罗马花椰菜是花椰菜(Brassica oleracea)的一个栽培品种。其显著的分形结构体现在圆锥形小花球的自相似排列中 —— 每个小花球都是整个花椰菜的微缩复制品,在多个尺度上重复着相同的螺旋模式。
照片由Victor Mozqueda提供(见致谢部分)
2.2 叶序
理解植物形态的第一步,是仔细观察并对所见之物进行分类。近距离观察会发现,叶片、花瓣和其他器官的位置并非随机,而是遵循着规律且往往重复的模式。早期植物学家通过耐心的测量与绘图发现,这些器官的生长角度和序列遵循着清晰的几何规律。
这促成了叶序学(phyllotaxis)的诞生 —— 该术语源自希腊语 “phyllon”(意为 “叶片”)和 “taxis”(意为 “排列”)。因此,叶序学指的是叶性器官(phyllomes)的有序排列。什么是叶性器官?叶性器官包含的主要器官有叶片、萼片、花瓣、雄蕊、心皮,以及其他从植物茎或轴上生长出的侧生附属结构。它们的空间排列方式决定了植物的叶序模式。

图 2.4:排列方式示例
(A)三月花葵,裂叶花葵(Lavatera trimestris,锦葵科),具 5 片花瓣
(B)全缘蜂兰(Ophrys holoserica,兰科),两侧对称花
(C)勋章菊(Gazania rigens,菊科)花序,具 13 枚舌状小花,呈斐波那契叶序;
(D)二列三毛草(Trisetum distichophyllum),具二列型(互生)叶序
(E)到手香(Plectranthus amboinicus,唇形科),具交互对生型(对生)叶序
(F)多叶芦荟(Aloë polyphylla),具螺旋叶序,顺时针方向有 5 条互生叶序线。
图源:[4] 由Didier Reinhardt提供
在二列型(distichous)排列中,连续的叶片沿着茎的两侧交替生长,彼此间隔 180 度。对生型(opposite)排列中,每个节上会长出一对叶片。当连续每对叶片的朝向相对于下方一对旋转 90 度时,便形成了交互对生型(decussate)排列,呈现出四条整齐的纵向列。若三个或更多叶片从同一个节上长出,则为轮生型(whorled)排列。然而,许多植物遵循互生型(alternate)或螺旋型(spiral)排列 —— 每个叶性器官与前一个之间保持固定的角度间隔,沿着茎呈螺旋路径缠绕生长。理解这些螺旋结构,是掌握叶序学的关键。


图 2.2:螺旋也十分常见
我们从标志性的向日葵花盘(Helianthus annuus)入手,探索螺旋结构(见图2.5)。花盘中心附近那些细小的凸起称为小花原基(floret primordia),这些原基日后会分化为完整的花朵,拥有自己的花冠、雄蕊和子房。

图 2.5:螺旋计数
观察向日葵花盘,我们可以绘制连接相邻小花的螺旋线。例如,左侧和右侧小图所示的另一个花盘上,我们数出 21 条和 34 条螺旋线,对应的互生叶序数为(21, 34)。
肉眼很容易发现,相邻的小花原基排列成相互交织的螺旋,从中心向外辐射。要数出图2.5中出现的螺旋数量,只需观察小花构成的可见曲线,沿顺时针或逆时针方向追踪,统计延伸至花盘边缘的不同螺旋数量即可。第一个令人惊讶的发现是:两个方向的螺旋数通常不同,例如一个方向有 21 条螺旋,另一个方向有 34 条。这些数字被称为互生叶序数(parastichy numbers)—— 即描述头状花序上可见的交错螺旋族的两个整数。
许多不同结构(如图2.6、2.7所示)都可以计算出这样的螺旋和互生叶序数。这些数字的系统性重复出现,早在很久以前就被人们注意到:公元前 300 年左右,泰奥弗拉斯托斯在《植物研究》中就提到了这种规律序列。当然,所有数学爱好者都会认出这些在植物中无处不在的特殊数字:2、3、5、8、13、21、34、55、89 等等。它们就是著名的斐波那契数列。
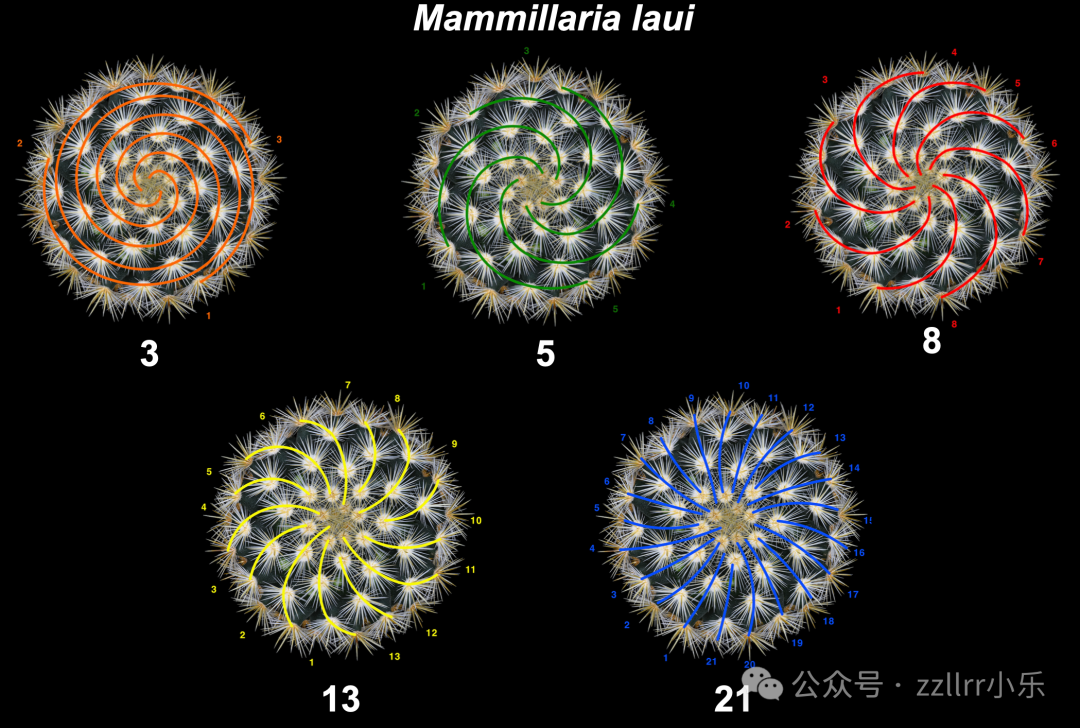
图 2.6:同一结构可具有多个互生叶序数
(图中植物名称:Mammillaria laui;标注数字:5、8、13、21)
照片由Victor Mozqueda提供(见致谢部分)
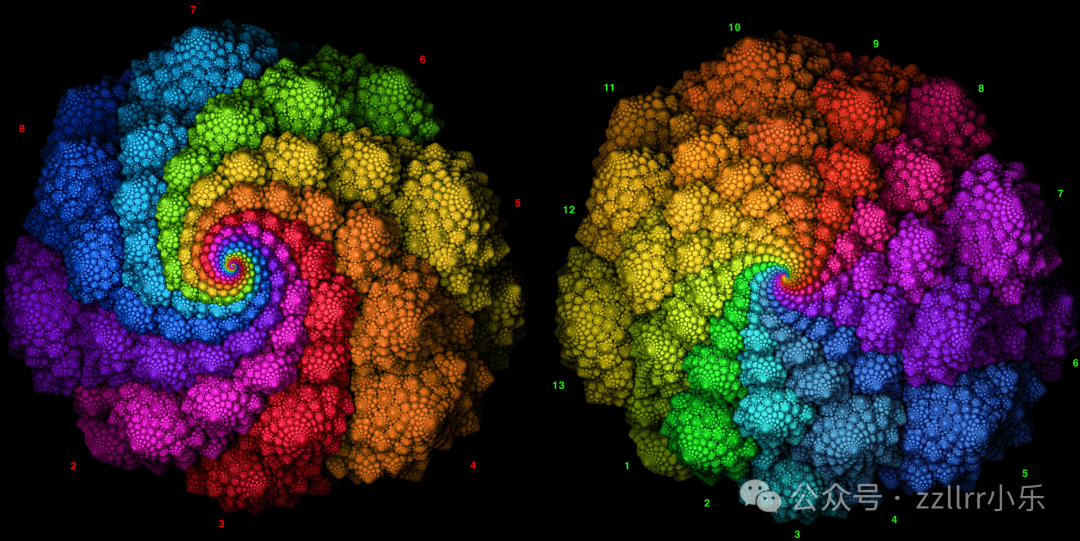
图 2.7:互生叶序数为 8 和 13 的罗马花椰菜
照片由Victor Mozqueda提供(见致谢部分)
斐波那契数列与植物的特殊关联,通常归功于约翰尼斯・开普勒(1611 年)—— 他在论文《论六角形的雪》(De nive sexangula)中研究自然对称性时,注意到了种子图案和松果中的这些数字。然而,直到 18 世纪中叶,植物学家才开始系统地记录植物中的这类模式。夏尔・博内(1754 年),以及后来的吉罗拉莫・萨凯里和约翰・克里斯蒂安・许布勒(19 世纪初),对叶片和种子的排列方式进行了定量研究。
令许多植物学家感到意外的是,这些数字的出现竟如此普遍。例如,在 1861 年写给美国伟大植物学家阿萨・格雷的一封信中,达尔文表达了他对理解这些数字的迫切渴望:“如果你想让我免于痛苦的死亡,就告诉我为什么会出现 1/2、1/3、2/5、3/8…… 这样的角度序列,而没有其他角度。这足以让最沉稳的人发疯。你和某位数学家是否发表过相关主题的论文?”
达尔文提到的角度问题,与我们的讨论密切相关。除了统计原基数量,我们还可以测量连续原基出现时的角间距。这一点在向日葵花盘上并不十分明显,但当我们直视茎轴上叶片的位置时,就会看得非常清楚。相邻两片叶子之间的夹角(即发散角)也呈现出极强的规律性。在许多螺旋叶序中,这个角度接近 137.5 度 —— 我们很快就会解释这个数字的由来。
2.3 点石成金
2.3.1 斐波那契数列与黄金比例
这些迷人的关联,为我们打开了一扇通往奇妙数学世界的大门。让我们从斐波那契数列开始。斐波那契数列是定义为{Fₙn≥0}的整数序列,其初始条件和递推关系如下:
F₀=0, F₁=1, 且对于n≥2,
Fₙ=Fₙ₋₁+Fₙ₋₂
因此,数列的前几项为:0、1、1、2、3、5、8、13、21、34、55……
现在,定义连续项的比值:
rₙ=Fₙ₊₁/Fₙ,(n≥1)
利用递推关系,我们可得:
rₙ=Fₙ₊₁/Fₙ=(Fₙ+Fₙ₋₁)/Fₙ
=1+Fₙ₋₁/Fₙ=1+1/rₙ₋₁
假设极限存在(这并非完全简单的推导)且不为零:
r=lim_{n→∞}rₙ
我们可以对关系式rₙ=1+1/rₙ₋₁取极限,得到:
r=1+1/r
两边同乘 r,得到二次方程:
r²−r−1=0
该方程的两个解为:
r=(1±√5)/2
由于所有rₙ >0,因此极限必为正根:
r=φ=(1+√5)/2
这就是黄金比例(golden ratio)。由于其在数学中的特殊地位,黄金比例有一个专属符号:φ。
2.3.2 连分数
黄金比例具有许多非凡的性质。让我们从其定义方程开始:
φ=1+1/φ
将等式右侧的 φ 替换为同一恒等式,可得:
φ=1+1/(1+1/φ)
再替换一次,得到三级表达式:
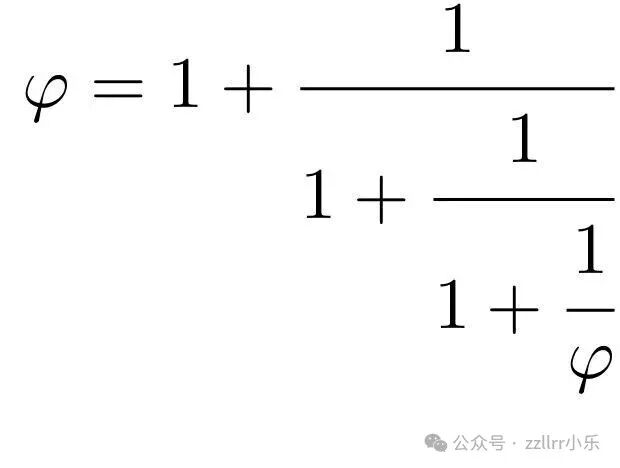
φ=1+1/(1+1/(1+1/φ))
更一般地,定义有限连分数逼近φₙ:
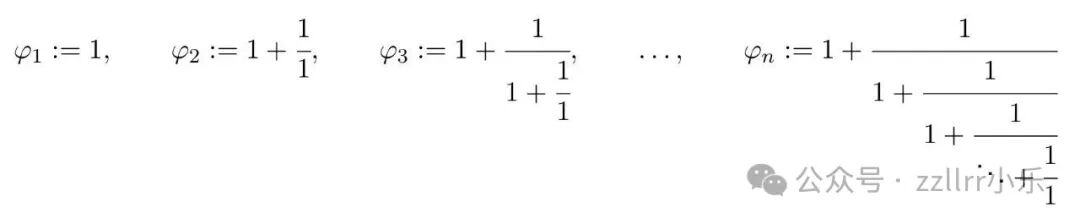
其中连分数中包含 n 项等于1。当n→∞时,极限将 φ 定义为无限简单连分数:
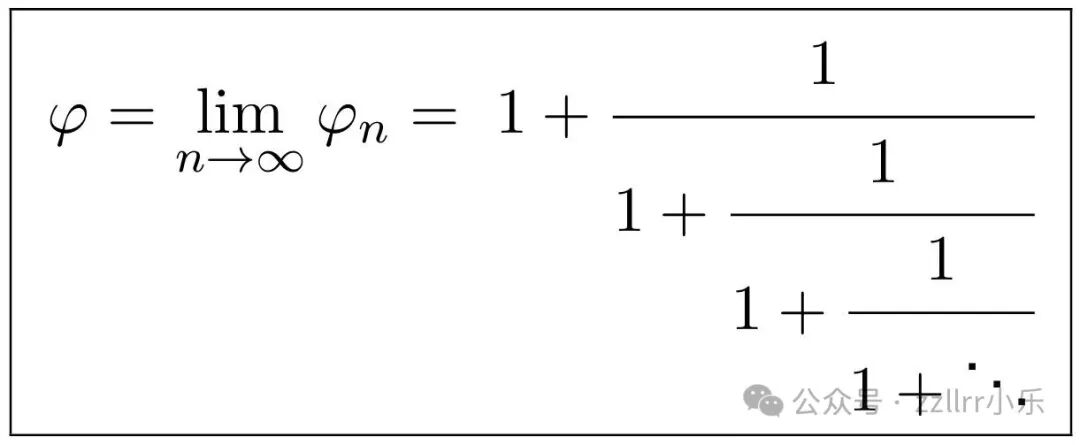
通常,我们用连分数符号简洁表示为:φ=[11,1,1,...]
在第 n 步截断,得到第 n 个收敛项:
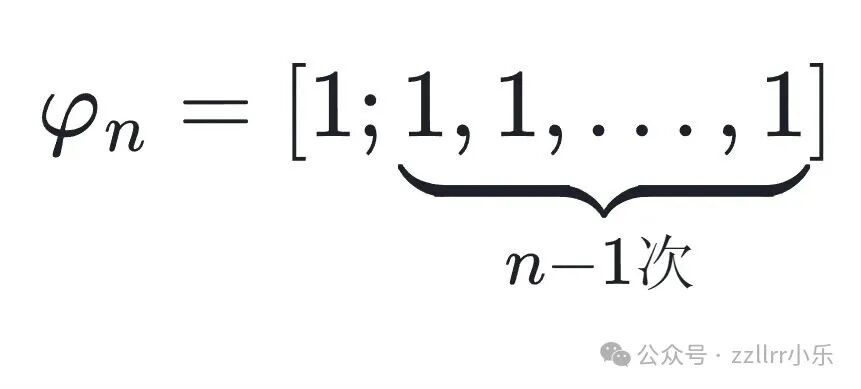
该收敛项可以表示为连续斐波那契数的比值:
φₙ = Fₙ₊₁/Fₙ
因此:
lim_{n→∞}φₙ=lim_{n→∞}Fₙ₊₁/Fₙ=φ
由此可见,截断 φ 的连分数表达式,自然会得到斐波那契比值序列。更一般地,连分数是一种具有以下形式的表达式:
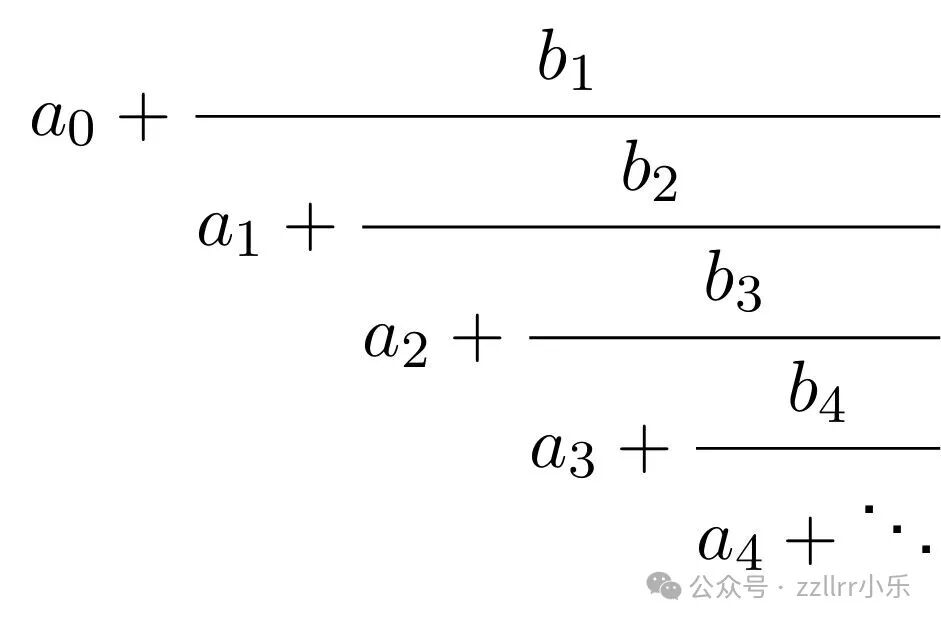
其中a₀, a₁, a₂, a₃, ... 和 b₁, b₂, b₃, ...为实数,且对于所有i≥1,均有aᵢ ≠ 0。
若表达式在有限步后终止,则称为有限连分数(此时若所有aᵢ 是有理数,此数就是有理数),否则称为无线连分数。以紧凑的记号将连分数写成:
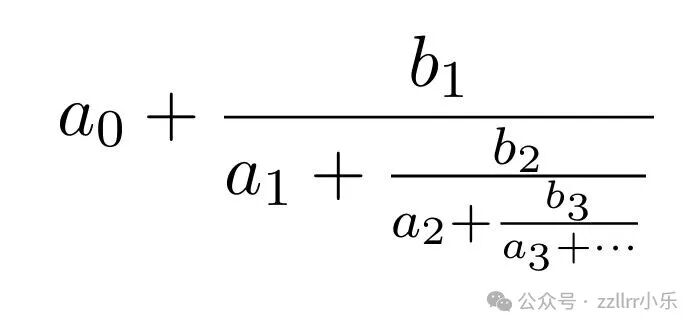
或者写成[a₀; a₁, a₂, a₃, ... ] 其中对所有i,bᵢ =1。
作为一个例子,留给读者一个练习是证明√2的连分数形式为:
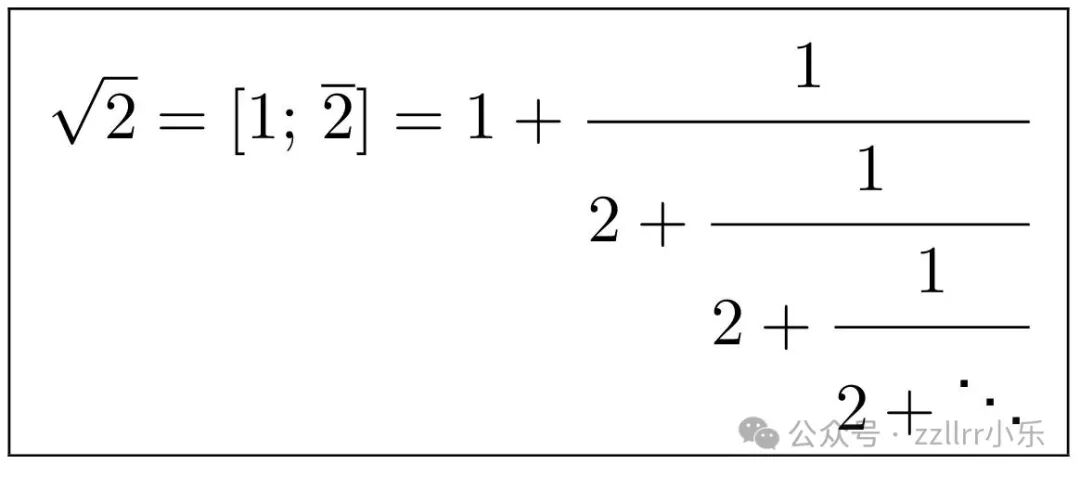
符号 [1; 2] 表示其中整数 2(2上面有上划线) 无限重复。该连分数快速收敛于√2=1.4142135...
2.3.3 黄金比例的几何性质
黄金比例还具有非凡的几何性质。首先,取一条总长度为 c 的线段,将其分为较长部分 a 和较短部分 b,因此:
c=a+b,b
我们提出一个简单的问题:找到比值a/b,使得 “较短部分与较长部分的比,等于较长部分与整体的比”。这可以转化为以下比例关系:
b/a=a/c=a/(b+a)
现在,引入比值:
φ:=c/a=a/b
由此可得a=φb。将其代入c=a+b,得到:
c=φb+b=(φ+1)b
因此:
φ=c/a=(φ+1)b/(φb)
=(φ+1)/φ=1+1/φ
我们再次得到了定义黄金比例的方程。
其次,考虑一个长方形,其长边长度为a+b,短边长度为 a(其中 a, b>0)。从长方形的一端移除一个边长为 a 的正方形,剩余的小长方形的边长为 a(长边)和 b(短边)。若这个小长方形与原长方形相似,则对应边的比值必须相等:
(a+b)/a=a/b
这再次定义了黄金比例和黄金矩形:若从黄金矩形中移除一个正方形,剩余的小长方形仍与原长方形相似,且这种比例关系会无限保持。
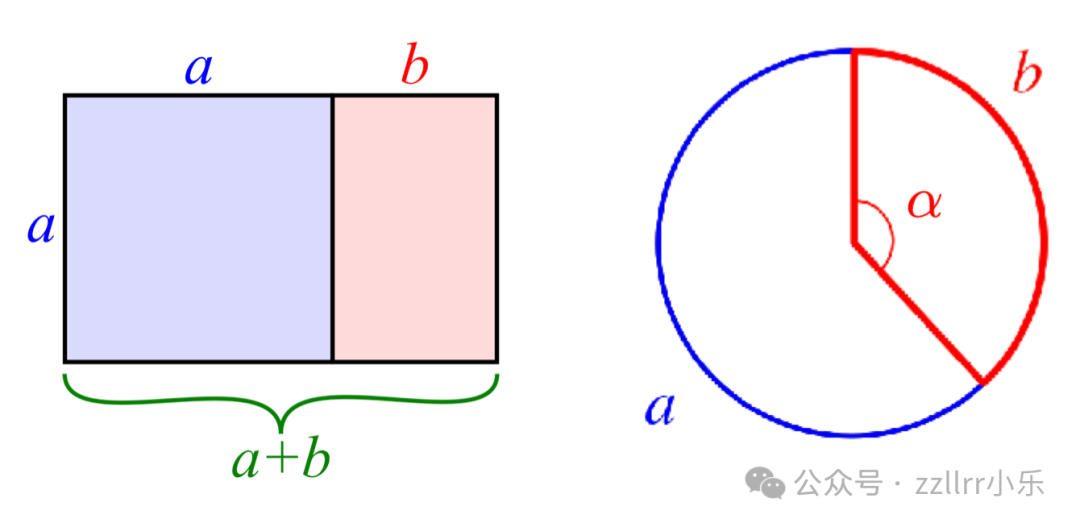
图 2.8:黄金比例在矩形和圆形上的特殊几何性质
(左)矩形:移除正方形后,剩余的小矩形与原矩形长宽比相同;
(右)圆形:定义黄金角 α。
现在,将同样的比例规则应用于圆的周长。将圆周长分为较长弧 a 和较短弧 b(其中b
若 φ 为黄金比例,则黄金角 α(以度和弧度为单位)为:
α = 360°/φ² ≈ 137.5077640°
α = 2π/φ² ≈ 2.39996323 rad(弧度)
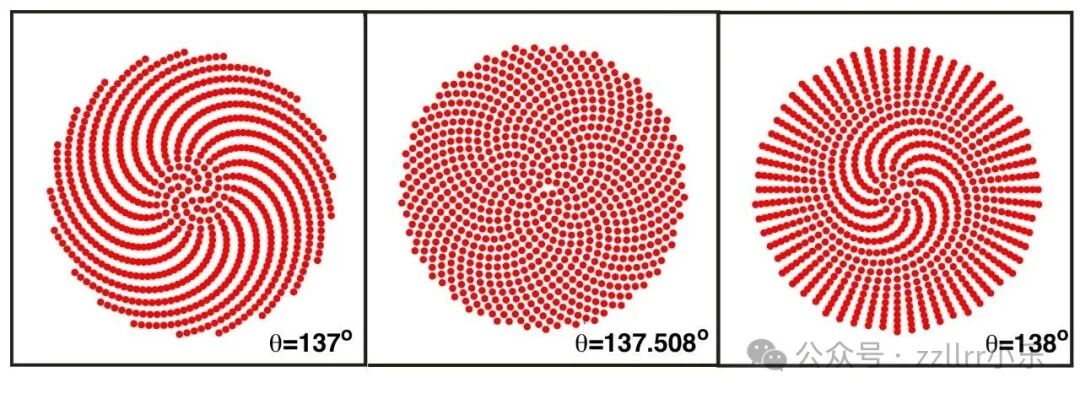
图 2.11:黄金角及邻近角度生成的排列模式
(从左至右:θ=137°、θ=137.508°、θ=138°)
至此,我们已经建立了斐波那契数列、黄金比例与黄金角之间的密切关联 —— 而黄金角,正是许多植物中出现的发散角!
2.4 发散螺旋
然而,这一切仍然让人觉得有些神秘。一方面,我们观察到相邻原基形成斐波那契螺旋;另一方面,连续原基的排列角度与黄金角相关。这两者之间存在怎样的联系?我们从一个简单的几何构造入手。
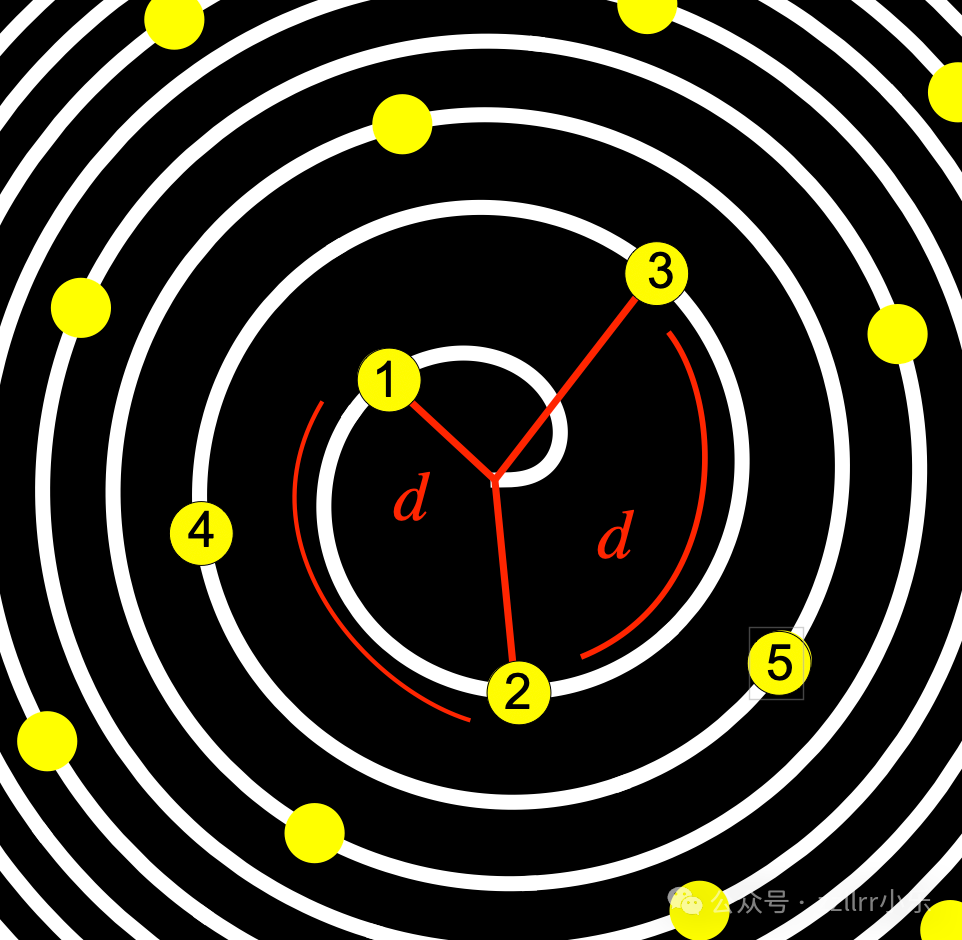
图 2.9:原基等角间距排列的费马螺旋示意图
标注为 1 的原基是最新形成的。
当新的原基在茎尖分生组织(SAM)中形成时,它们会被向外输送。我们将原基的沉积模拟为出现在一条螺旋线上 —— 这并非相邻原基形成的斐波那契螺旋,而是图2.9所示的费马(抛物线)螺旋:
r(θ)=c√θ,c>0,θ≥0
接下来,我们将原基依次放置在固定的发散角 d 处,令:
θₙ=nd,
n=1,2,3,...(索引脚标n=0对应圆心)
请注意,原基的编号与沉积顺序相反(n=1为最新沉积的原基)。因此,第 n 个原基的半径为:
rₙ=c√θₙ=c√(nd)
其直角坐标为:
xₙ=rₙcosθₙ=c√(nd) cos(nd)
yₙ =rₙsinθₙ=c√(nd) sin(nd)
这种选择使得每个原基占据的面积大致相等。事实上:
ΔAₙ=π(rₙ₊₁²−rₙ²)
=πc²((n+1)d−nd)=πc²d
该值对于所有 n 均为常数。
现在,若我们选择d=360°/N(其中 N>0 为整数),将会看到 N 条臂状结构出现(如图2.10所示)。
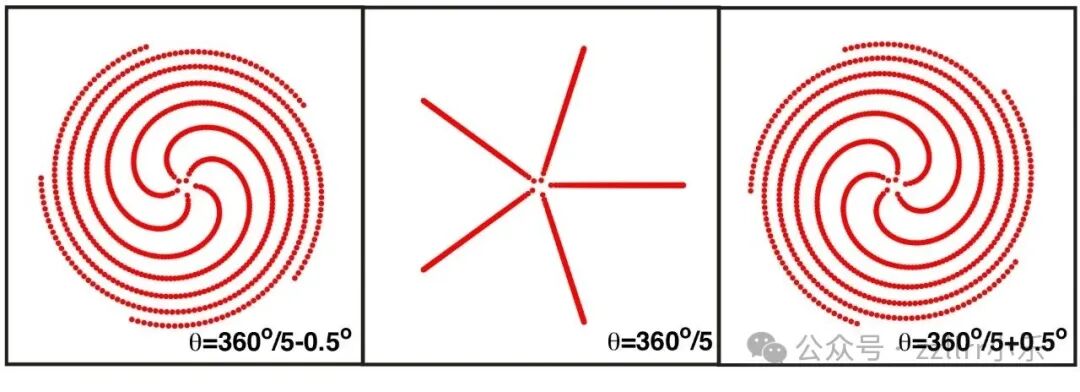
图 2.10:发散角对排列模式的影响
选择d=360°/5会形成5臂结构;发散角略微减小或增大 0.5 度,会分别形成右旋或左旋的5臂螺旋。
接下来,让我们看看当我们将 d 设为黄金角 α (如图2.8所示)时会发生什么。显然,这种模式能很好地填满不断生长的圆盘,没有空隙 —— 当观察相邻角度时,这一点尤为明显。我们发现,这种排列方式的堆积效率极高,且可见的互生叶序数接近连续的斐波那契数。
若d/2π为有理数(例如p/q),则经过 q 步后,这些点将回到接近相同的方向,形成 q 条不同的径向线,且线之间会留下较大空隙。然而,当d/2π为无理数时,这些点永远不会完全重复,能更均匀地填满圆盘。值得注意的是,最均匀、无空隙的排列恰好出现在黄金角的情况下。这是因为黄金比例是 “最无理” 的数 —— 从连分数的角度来看,它的有理数逼近速度最慢。因此,没有任何两个原基会紧密对齐,堆积方式也尽可能均匀、高效。
2.4.1 茎尖分生组织的芽形成机制
上述构造是几何化且描述性的。它解释了观察到的不同数量之间的关系,但并未解释芽最初在茎尖分生组织上的形成位置 —— 我们只是简单地假设了它们基于螺旋线的位置。
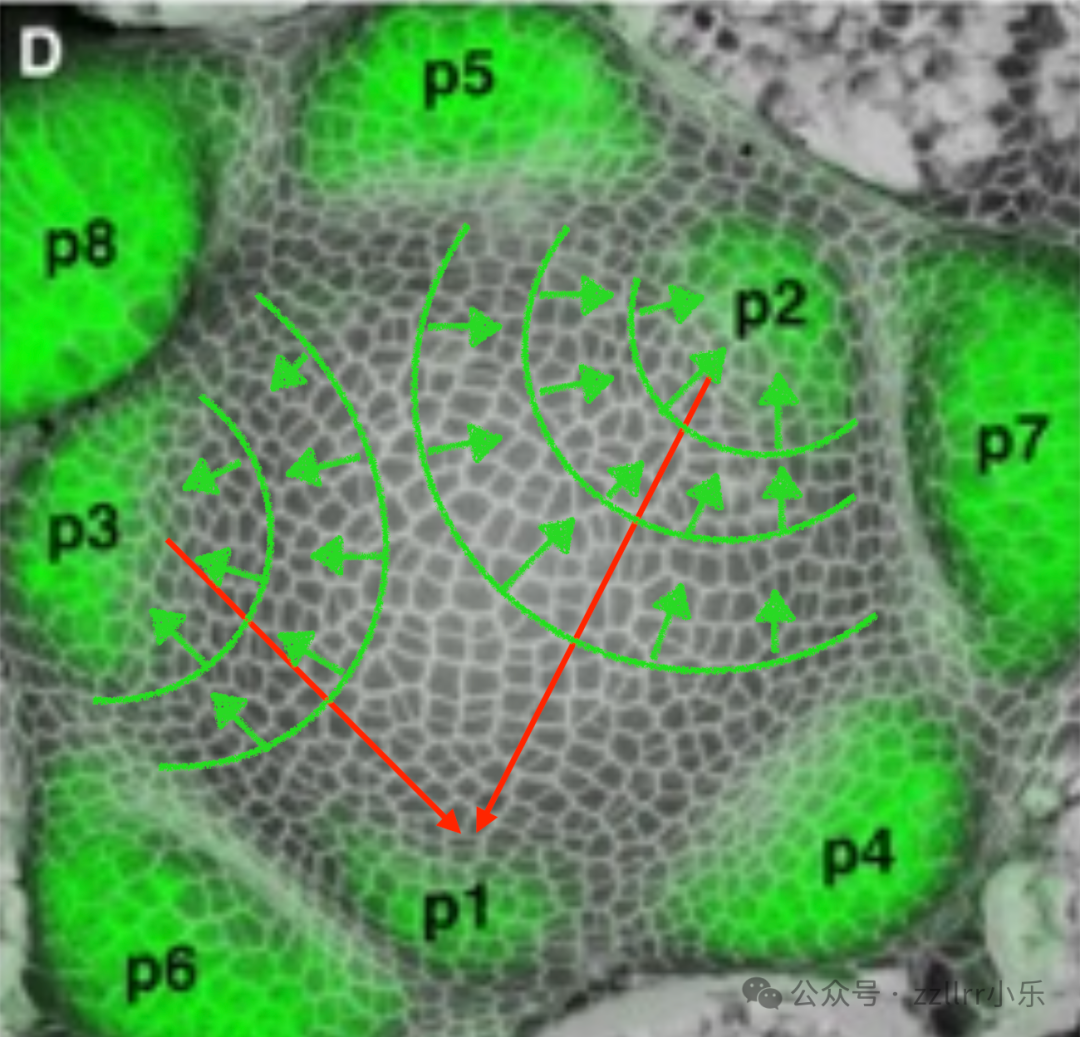
图 2.12:茎尖分生组织的原基形成
新原基(P1)在生长素浓度最高的位置形成,该位置也是距离前两个吸收生长素的原基(P2 和 P3)最远的点。
在生长中的茎尖,茎尖分生组织通过原基的局部启动,持续产生新的器官(叶片、苞片或小花)。这一过程由植物激素生长素(一种通用的植物形态发生素)调控。生长素通过松弛细胞壁来刺激植物细胞变形:它激活质膜上的质子泵,降低细胞壁区域的 pH 值,从而激活能够破坏纤维素微纤丝之间氢键的酶(扩张蛋白),使细胞壁在内部膨压下伸展。因此,新芽的位置由局部生长素浓度决定。
生长素通过特定的载体蛋白(PIN 转运蛋白)在细胞间主动运输,在分生组织表面形成动态流动。正在发育的现有原基会充当生长素库,将激素从其周围区域吸走。结果,现有芽附近的生长素浓度最低,而在更远的区域,生长素浓度逐渐升高。
新的原基在生长素浓度达到局部最大值的位置启动 —— 也就是离现有原基影响最远的位置。这种自组织机制会自动将新芽定位在与早期芽距离最远的位置,在茎尖周围形成发散排列。
在包含化学运输、细胞机械扩张和分裂的生长茎模型中,从数学和几何角度实施这一规则,会产生螺旋叶序:每个新原基出现的角度位置,都会避免与之前的原基重叠。计算模型已证实了这种涌现行为 —— 基于这些规律,黄金角 [图2.8]会自然出现。
尽管黄金角在植物中分布极为广泛,但其选择优势仍不明确。人们曾认为,它通过排列叶片以最小化遮挡来优化光照捕获,但实验模型表明,其他发散角也能达到类似的效率。同样,虽然黄金角能使种子和小花实现致密堆积,但仅靠高效堆积无法解释它在叶片等结构中的存在 —— 在这些结构中,机械约束或发育限制可能更为重要。
尽管存在许多数学和生理学模型,但尚未出现明确的进化解释。因此,黄金角在不同植物物种中的反复出现,仍是植物进化和形态发生学中一个持久的谜团。
致谢
我非常荣幸地感谢维克多・莫兹奎达(Victor Mozqueda),他慷慨地与我分享了他精彩的摄影作品。你可以在他的 Instagram 页面上了解更多相关作品:https://www.instagram.com/plantsandbugs/
2.5 延伸阅读
关于叶序模式的精彩探索,可参见《植物懂数学吗?—— 解开植物螺旋的奥秘,从列奥纳多・达・芬奇到如今》(Do Plants Know Math?: Unwinding the Story of Plant Spirals, from Leonardo da Vinci to Now,2024)[1]。对于数学基础更扎实的读者,《数学叶序学》(Mathematical Phyllotaxis)一书深入探讨了所有细节。
探索植物与数学的经典著作包括《植物的算法之美》(The Algorithmic Beauty of Plants,1990)[3]。
卡尔・J・尼克拉斯(Karl J. Niklas)的《植物生物力学》(Plant Biomechanics)是一部更深入、更定量的著作,探讨了物理原理和机械约束如何塑造植物形态,为希望超越通俗读物、寻求更深入科学理解的读者提供了严谨的基础 [2]。
原文参考文献
[1] 斯特凡纳・杜阿迪(Stéphane Douady)、雅克・杜梅(Jacques Dumais)、克里斯托夫・戈莱(Christophe Golé)、南希・皮克(Nancy Pick). 《植物懂数学吗?—— 解开植物螺旋的奥秘,从列奥纳多・达・芬奇到如今》(Do Plants Know Math?: Unwinding the Story of Plant Spirals, from Leonardo da Vinci to Now). 普林斯顿大学出版社,新泽西州普林斯顿,2024
[2] 卡尔・J・尼克拉斯(Karl J. Niklas). 《植物生物力学:植物形态与功能的工程学视角》(Plant Biomechanics: An Engineering Approach to Plant Form and Function). 芝加哥大学出版社,芝加哥,1992
[3] 普热梅斯瓦夫・普鲁辛凯维奇(Przemyslaw Prusinkiewicz)、阿里斯泰德・林登迈尔(Aristid Lindenmayer). 《植物的算法之美》(The Algorithmic Beauty of Plants). 虚拟实验室。施普林格出版社,纽约,1990
[4] 迪迪埃・莱因哈特(Didier Reinhardt)、埃迪塔・M・戈拉(Edyta M Gola). 植物中的规律与秩序 —— 叶序的起源及其功能相关性(Law and order in plants–the origin and functional relevance of phyllotaxis). 《植物科学趋势》(Trends in Plant Science),27 (10):1017-1032,2022
[5] 理查德・S・史密斯(Richard S. Smith)、索阿齐格・居约马尔克(Soazig Guyomarc’h)、泰蕾兹・曼德尔(Thérèse Mandel)、迪迪埃・莱因哈特(Didier Reinhardt)、克里斯・库赫莱梅尔(Cris Kuhlemeier)、普热梅斯瓦夫・普鲁辛凯维奇(Przemyslaw Prusinkiewicz). 一种合理的叶序模型(A plausible model of phyllotaxis). 《美国国家科学院院刊》(Proceedings of the National Academy of Sciences of the United States of America),103 (5):1301-1306,2006.
[1] Stéphane Douady, Jacques Dumais, Christophe Golé, and Nancy Pick. Do Plants Know Math?: Unwinding the Story of Plant Spirals, from Leonardo da Vinci to Now. Princeton University Press, Princeton, NJ, 2024
[2] Karl J. Niklas. Plant Biomechanics: An Engineering Approach to Plant Form and Function. University of Chicago Press, Chicago, 1992
[3] Przemyslaw Prusinkiewicz and Aristid Lindenmayer. The Algorithmic Beauty of Plants. The Virtual Laboratory. Springer-Verlag, New York, 1990
[4] Didier Reinhardt and Edyta M Gola. Law and order in plants–the origin and functional relevance of phyllotaxis. Trends in Plant Science, 27(10):1017–1032, 2022
[5] Richard S. Smith, Soazig Guyomarc’h, Thérèse Mandel, Didier Reinhardt, Cris Kuhlemeier, and Przemyslaw Prusinkiewicz. A plausible model of phyllotaxis. Proceedings of the National Academy of Sciences of the United States of America, 103(5):1301–1306, 2006
© 阿兰・戈里利教授 2025-2026 年
参考资料
https://www.gresham.ac.uk/sites/default/files/transcript/R_2025_11_06_1152_Goriely_T%20final.pdf
https://www.gresham.ac.uk/watch-now/shape-plants
https://www.gresham.ac.uk/watch-now/series/geometry-nature

