还别不信,这道数格子的数学竞赛题真能把人数晕
原创 Helen 罗博深数学
 今天我们要讲的题目是2022年AMC 8的第23题。
今天我们要讲的题目是2022年AMC 8的第23题。这道题目是一道比较有代表性的排列组合题。每年的AMC 8后5题都是比较有难度的。这道题是不是看起来也有点无从下手?不过不要被吓到,我们自有巧妙办法!
原题:
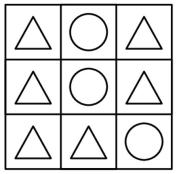
A △ or ◯ is placed in each of the nine squares in a 3-by-3 grid. Shown below is a sample configuration with three △s in a line. How many configurations will have three △s in a line and three ◯s in a line?
中文译题:
在一个九宫格内,每一格中可以放置△或◯中的任意一个图形。下图的例子中三个△连成了一条直线。那么一共有多少种九宫格排列中,会出现三个△组成的直线和三个◯组成的直线?
 题目解析
题目解析今天的题目是一道典型的排列组合题。
首先,我们通过观察得知,不可能有一条横格和一条竖格子同时出现△和◯,因为它们必然有一个共用的交点。
那么满足问题的只可能有两条横格或者两条竖格。
考虑到一个九宫格旋转九十度之后竖格就会变成横格,所以我们只需要考虑竖格的情况,因为横格的情况应该是一一对应的。
我们可以考虑两种情况,第一种是三条格子都是△直线或◯直线的情况。如下图。
每一条格,都有两种图形可以选。那么三条直线就有2x2x2=8种排列方法。
值得注意的是,其中有两种是不能算在内的,分别是全部△和◯的情况。
所以一共应该有8-2 = 6种。
第二种是两条是△直线或◯直线,第三条△和◯混合的情况。
因为图形里只有两条全△或全◯直线,并且△和◯各自只能有一条直线,所以第一条直线可以选择的位置有3个(第一列,第二列,第三列)。
第二条直线只能选剩下的2个位置中的一个。
所以一共有3!= 6种不同的组合。
剩下的三格中有2x2x2=8种不同的组合方式,因为每一格可以选两个图形。
但是有两种全部△和◯的情况需要排除在外,所以是8-2 = 6种不同组合方式。那么一共就有6x6=36种。
两种情况组合起来就是36+6 = 42。再算上横格的情况就是42x2=84种。
另一种解法
这种考虑的方法很细致,但是步骤多。
还有另一种简便的考虑方法,但是容易多数,这里也简单介绍一下。因为我们只在意直线的情况,那么
有三个位置可以选择, 分别是第一列,第二列,第三列,那么
可以选剩下两列。
所以一共有2x3=6种不同的排列方法。
剩下的三个方格则有2x2x2=8种不同的方法。
所以共有6x8=48种。
这种考虑方法有一个难点,数到这里我们发现每一个有两列相同图形和一列不同图形例如下图的情况都被考虑了两次。
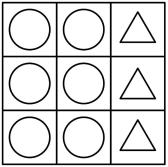 而这种情况出现了3x2=6次。所以我们知道有48-6=42种不同的排列方式。和之前一样,算上横线的部分是42x2=84种。
而这种情况出现了3x2=6次。所以我们知道有48-6=42种不同的排列方式。和之前一样,算上横线的部分是42x2=84种。你想明白了吗?
原标题:《还别不信,这道数格子的数学竞赛题真能把人数晕》

