量子力学诠释问题
以下文章来源于中国物理学会期刊网 ,作者孙昌璞
中国物理学会期刊网.
中国物理学会期刊网(www.cpsjournals.cn)是我国最权威的物理学综合信息网站,有物理期刊集群、精品报告视频、热点专题网页、海内外新闻、学术讲座,会议展览培训、人物访谈等栏目,是为物理学习和工作者提供一站式信息服务的公众平台。
|作者:孙昌璞1,2
(1 中国工程物理研究院研究生院)
(2 北京计算科学研究中心)
本文发表于《物理》2017年第8期
■推荐理由
作者讨论了量子力学的深层次理解,对于学界一些偏离的提法进行了纠正。
摘 要 量子力学的建立不仅奠定了当代科学的基础,而且在推动当代技术革命方面取得了惊人的成功。然而,对于量子力学诠释(interpretation of quantum mechanics)——理解波函数如何刻画微观世界,人们迄今为止并未形成共识。量子力学发展的这种二元状态不仅带来了认识论方面的误导,而且依据备受争议的哥本哈根诠释建立起来的量子技术会有许多根本性问题。
量子力学的哥本哈根诠释存在二元结构的问题:微观世界的运动用量子力学描述,是一个幺正演化,而观察或测量却依赖于量子系统外部的经典世界(仪器、观察者、环境),表现出来的波包塌缩是非幺正的。为此,包括爱因斯坦、薛定谔、温伯格等在内的一些著名学者对哥本哈根诠释提出了尖锐的批评。80年过去了,为克服量子力学的哥本哈根诠释二元论困境,人们提出各种各样的量子力学诠释,包括多世界诠释、量子退相干诠释、自洽历史诠释以及量子达尔文主义等。文章将简要介绍和评述这些量子力学诠释的基本思想、它们之间的逻辑关系及其实验检验的可能性。进一步澄清量子力学诠释中的基本概念,可以避免量子观念滥用导致的意识论上的问题和量子技术发展误入歧途。
关键词 量子力学诠释,二元结构,哥本哈根诠释,多世界诠释,量子退相干, 自洽历史,量子达尔文主义
01
引言:量子力学的二元结构和其发展的二元状态
上世纪二十年代, 海森伯(Werner Karl Heisenberg)、薛定谔(Erwin Schrödinger) 和玻恩(Max Born)等人创立了量子力学,奠定了人类认识微观世界的科学基础,直接推动了核能、激光和半导体等现代技术的创新,深刻地变革了人类社会的生活方式。量子力学成功地预言了各种物理效应并解释了诸多方面科学实验,成为当代物质科学发展的基石。然而,作为量子力学核心观念的波函数在实际中的意义如何,自爱因斯坦(Albert Einstein) 和玻尔(Niels Bohr) 旷世之争以来,人们众说纷纭,各执一词,并无共识。可以说,直到今天,量子力学发展还是处在一种令人尴尬的二元状态:在应用方面一路高歌猛进,在基础概念方面却莫衷一是。这种二元状态,看上去十分之不协调。对此有人以玻尔的“互补性”或严肃或诙谐地调侃之,以“shut up and calculate”的工具主义观点处之以举重若轻[1—9]。
然而,对待量子力学诠释严肃的科学态度应该是首先厘清量子力学诠释中哪一部分观念导致了基本应用方面的“高歌猛进”,哪一部分观念导致了理解诠释方面的“莫衷一是”。对量子力学诠释不分清楚彼此、逻辑上倒因为果的情绪化评价,会在概念上混淆是非,误导量子理论与技术的真正创新。无怪乎,有人以“量子”的名义为认识论中“意识可以脱离物质”的明显错误而张目,其根源就是每个人心目中有不同的量子力学诠释。
我个人认为,这样一个二元状态主要是由于附加在玻恩几率解释之上的“哥本哈根诠释”之独有的部分:外部经典世界存在是诠释量子力学所必需的,是它产生了不服从薛定谔方程幺正演化的波包塌缩,使得量子力学二元化了。今天,虽然波包塌缩概念广被争议,它导致的后选择“技术”却被广泛地应用于量子信息技术的各个方面,如线性光学量子计算和量子离物传态的某些实验演示。
其实,我以上的观点契合了来自一些伟大科学家的伟大声音!现在,让我们再一次倾听来自量子力学创立者薛定谔对哥本哈根诠释直言不讳的批评。早年,薛定谔曾经写信严厉批评了当时的物理学家们[10],因为在他看来,他们不假思索地接受了哥本哈根解释:“除了很少的例外(比如爱因斯坦和劳厄(Max von Laue)),所有剩下的理论物理学家都是十足的蠢货,而我是唯一一个清醒的人”。薛定谔在写给他老朋友玻恩的一封信中说:
“我确实需要给你彻底洗脑……你轻率地常常宣称哥本哈根解释实际上已经被普遍接受,毫无保留地这样宣称,甚至是在一群外行人面前——他们完全在你的掌握之中。这已经是道德底线了……你真的如此确信人类很快就会屈从于你的愚蠢吗?”
薛定谔传记作者约翰·格里宾(John Gribbin)看到这些信,感叹道:“作为一位在仅仅几年后就接受了哥本哈根解释的教导,并且直到很久之后才意识到这种愚蠢的人,我发现薛定谔在1960 年的这些话直击我心!”
1979 年诺奖得主、物理学标准模型的奠基者之一史蒂文·温伯格(Steven Weinberg)在《爱因斯坦的错误》一文中,很具体、很直接地批评了哥本哈根诠释的倡导者玻尔对于测量过程的不当处理[11]:
“量子经典诠释的玻尔版本有很大的瑕疵,其原因并非爱因斯坦所想象的。哥本哈根诠释试图描述观测(量子系统)所发生的状况,却经典地处理观察者与测量的过程。这种处理方法肯定不对:观察者与他们的仪器也得遵守同样的量子力学规则,正如宇宙的每一个量子系统都必须遵守量子力学规则。”“哥本哈根诠释明显地可以解释量子系统的量子行为,但它并没有达成解释的任务,那就是应用波函数演化确定性方程(薛定谔方程)于观察者和他们的仪器。”
最近温伯格先生又进一步强调了他对“标准”量子力学的种种不满[12,13]。对哥本哈根诠释的严肃批评自其出笼至今就不绝于耳,但也有不少人却充耳不闻,这显然是一种选择性失聪!在量子信息领域,不少人不加甄别地使用哥本哈根诠释导致的“后选择”方案,其可靠性、安全性必然令人生疑!
其实,在量子力学幺正演化的框架内,多世界诠释[14—21]不引入任何附加的假设,成功地描述了测量问题,从而对哥本哈根诠释系统而深入的挑战。需要指出的是,此前不久建议的隐变量理论[22,23]在理论体系上超越了量子力学框架,本质上是比量子力学更基本的理论,因此对此进行检验的Bell 不等式本文不予系统讨论。自上一世纪八十年代初,人们提出了各种看似形式迥异的量子力学诠释,如退相干理论[3, 4, 24—28]、自洽历史诠释[29,30]、粗粒化退相干历史[31,32]和量子达尔文主义。后来经深入研究, 人们意识到,这些诠释大致上是多世界诠释思想的拓展和推广。
02
哥本哈根诠释及其推论
哥本哈根诠释是由玻尔和海森伯等人在1925—1927 年间发展起来的量子力学的一种诠释。它对玻恩所提出的波函数的几率解释进行了超越经典几率诠释的推广,突出强调了波粒二象性和不确定性原理。虽然人们心目中量子力学哥本哈根诠释有各种各样版本,但对其核心内容人们还是有所共识的,那就是“诠释量子世界,外部的经典世界必不可少”。
大家知道,微观世界运动基本规律服从薛定谔方程,可以用演化波函数描述;等效地,也可以用涉及不可对易力学量的运动方程和系统定态波函数。这两种运动方程描述都保证了波函数服从态叠加原理:如果|ϕ1> 和|ϕ2> 满足运动方程,则
(1)
也是微观世界满足运动方程的可能状态。当|ϕ1> 和|ϕ2> 是某一个力学量的本征态(对应本征值a1和a2),则根据玻恩几率解释,对|ϕ> 测量A 的可能值只能随机地得到a1和a2,相应的几率是|c1|2 和|c2|2 。因而,A平均值是
(2)
这就是玻恩几率解释的全部内容,不必附加任何假设,足以用它理解微观世界迄今为止所有的实验数据。
结合量子力学的数学框架中波函数假设和基本运动方程,玻恩几率解释构成了量子力学的基本内容,可以正确预言从基本粒子到宏观固体的诸多物理特性和效应。但哥本哈根诠释却要通过附加的假设拓展玻恩几率解释。这个拓展从冯·诺依曼(John von Neumann)开始,追问测量后的波函数是什么[33]。这个追问满足了人们对终极问题的刨根问底,同时物理上的诉求也是合情合理的,即,对紧接着的重复测量测后系统给出相同的结果。
冯·诺依曼首先把测量定义为相互作用产生的仪器(D)和系统(S)的关联(也可以笼统地叫做纠缠)。特殊相互作用导致的总系统D+S 演化波函数为
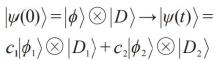
(3)
根据上面的方程,一旦观察者发现了仪器在具有特制经典的态|D1> 上, 则整个波函数塌缩到|ϕ1>⊗ |D1> ,从而由仪器状态D1 读出系统状态|ϕ1> ,对|ϕ2> 亦然。自此,哥本哈根学派或与有关人士把这种波包塌缩现象简化为一个不能由薛定谔方程描述的非幺正过程:在|ϕ> 上测A,测量一旦得到结果a1,则测量后的波函数变为|ϕ> 的一个分支|ϕ1> 。这个假设的确保证了紧接着的重复测量给出相同的结果。
然而,玻尔从来都不满足于物理层面上的直观描述和数学上的严谨表达,对于类似波包塌缩的神秘行为他进行了“哲学”高度的提升:只有外部经典世界的存在,才能引起波包塌缩这种非幺正变化,外部经典世界是诠释量子力学所必不可少的。
加上波包塌缩假设,人们把量子力学诠释归纳为以下6条[34]:
(1)量子系统的状态用满足薛定谔方程的波函数来描述,它代表一个观察者对于量子系统所能知道的全部知识(薛定谔);
(2)量子力学对微观的描述本质上是概率性的,一个事件发生的概率是其对应的波函数分量的绝对值平方(玻恩);
(3)力学量用满足一定对易关系的算符描述,它导致不确定性原理:一个量子粒子的位置和动量无法同时被准确测量(海森伯), Δx Δp ≥ℏ/2;
(4)互补原理(Complementarity principle,亦译为并协原理):物质具有波粒二象性,一个实验可以展现物质的粒子行为或波动行为,但二者不能同时出现(玻尔);
(5)对应原理:大尺度宏观体系的量子行为接近经典行为(玻尔);
(6)外部经典世界是诠释量子力学所必需的,测量仪器必须是经典的(玻尔与海森伯)。
一般说来,“哥本哈根诠释”特指上述6 条量子力学基本原理中的后4 条。然而,玻尔等提出的4条“军规”,看似语出惊人,实质却可证明为前两条的演绎。第3 条海森伯不确定性关系并不独立于玻恩几率解释。只是由于不确定关系能够凸显量子力学的基本特性——不能同时用坐标和动量定义微观粒子轨道,看上去立意高远!玻尔和海森伯等从哲学的高度把它提升到量子力学的核心地位。但是,今天大家意识到,只要用波函数玻恩解释给出力学量平均值公式,就可以严格导出不确定关系。其实,在研究具体问题时,不确定性关系可以解释一些新奇的量子效应,但不能指望它给出所有精准的定量预言。
哥本哈根“军规”第4 条——玻尔互补原理后半句话“波动性和粒子性在同一个实验中,二者互相排斥、不可同时出现”经常被人们忽略,但它却是互补原理的精髓所在。玻尔互补原理在一定的意义上可以视为哲学性的描述。玻尔本人甚至认为可以推广到心理学乃至社会学,以彰显其普遍性!然而,虽然它看似寓意深奥,在操作层面上却不完全独立于不确定性关系。量子力学的奠基者之一、也被视为哥本哈根学派主力的保罗·狄拉克(Paul Dirac)对此有不屑的态度[35]。对于玻尔那种主要表现在互补原理之中的“啰嗦的、朦胧的”哲学,狄拉克根本无法习惯。1963年,狄拉克谈到互补原理时说,“我一点也不喜欢它”,“ 它没有给你提供任何以前没有的公式”。狄拉克不喜欢这个原理的充分理由,从侧面反映了互补原理不是一般的可以用数学准确表达的物理学结论。其实,尽管互补原理不能吸引狄拉克,但也许还是潜移默化地影响了他的思维,在狄拉克《量子力学原理》前言当中及其他地方,他强调的不变变换可以看做是玻尔互补观念的一种表现。
其实,我们能够清晰地展示互补原理的不独立性。在粒子双缝干涉实验中,要探知粒子路径意味着实验强调粒子性,波动性自然消失,干涉条纹也随之消失,发生了退相干。玻尔互补原理对此进行了哲学高度的诠释:谈论粒子走哪一条缝,是在强调粒子性,因为只有粒子才有位置描述;强调粒子性,波动性消失了,随即也就退相干了。海森伯用自己的不确定性关系对这种退相干现象给出了比较物理的解释:探测粒子经过哪一条缝,相当于对粒子的位置进行精确测量,从而对粒子的动量产生很大的扰动,而动量联系于粒子物质波的波矢或波长,从而导致干涉条纹消失。海森伯本人认为,通过不确定性关系很好地印证了互补性原理。然而,玻尔并不买海森伯的帐,认为只有互补原理才是观察引起退相干问题的核心,测量装置的预先设置决定了“看到”的结果。强调不确定性关系推导出互补性,本质上降低了理论的高度和深度。当然,玻尔本人也认为不确定性关系是波粒二象性的很好展现:Δx 很小,意味着位置确定,这对应着粒子性,这时Δp 很大,波矢不确定所以波动性消失了。哥本哈根“军规”第5 条是对应原理,它可以视为薛定谔方程半经典近似的结果。
经过这样的分析甄别,可以断定只有第6 条才是“哥本哈根诠释”独特且独立的部分,也正是它导致了量子力学诠释的二元论结构:微观系统服从导致幺正演化的薛定谔方程(U 过程),但对微观系统测量过程的描述则必须借助于经典世界,它导致非幺正的突变(R 过程)。罗杰·彭罗斯(Roger Penrose)多次强调,量子力学哥本哈根诠释的全部奥秘在于量子力学是否存在薛定谔方程U过程以外的R过程。
当年,玻尔认为这种描述是十分自然的:为了获取原子微观世界的知识,对于生活在经典世界的人类而言,所用的仪器必须是经典的。然而,仪器本身是由微观系统组成,每一个粒子服从量子力学,经典与量子之间必存在边界,但边界却是模糊的。哥本哈根诠释要想自洽,就要根据实际需要调整边界的位置,可以在仪器—系统之间,可以在仪器—人类观察者之间,甚至可以是视觉神经和人脑之间。
如果说“边界可变”的哥本哈根诠释是一条灵动而有毒的“蛇”,哥本哈根“军规”第6 条是其最核心、最致命的地方。温伯格先生对此的严厉批评和质疑,正好打了“蛇”的七寸。七寸处之“毒”在意识论上会导致冯·诺依曼链佯谬:人的意识导致最终波包塌缩。让我们考察冯·诺依曼量子测量的引申。我们不妨先承认玻尔的“经典必要性”。如果第一个仪器用量子态描述,为什么系统+仪器的复合态会塌缩到|ϕ1> ⊗ |D1> ,答案自然是有第二个经典仪器D2 存在,使得更大的总系统塌缩到|ϕ1> ⊗ |D1> ⊗ |D2> ⋯ 。以此类推要塌缩到以下链式分支上:
(4)
据此类推,最末端的仪器在哪里呢?那么,要想有终极的塌缩, 末端必须是非物质“ 神” 或“人”的意识。冯·诺依曼的好友维格纳(Eugene Wigner)就是这样推断意识会进入物质世界[36]。
我个人猜想,目前国内有人由量子力学论及“意识可独立于物质而存在”,正是拾维格纳的牙慧,把哥本哈根诠释进行这种不合理的逻辑外推。然而,这个结论逻辑上是有问题的,如果我们研究的系统是整个宇宙,难道有宇宙之外的上帝?对此的正确分析可能要涉及一个深刻的数学理论:随着仪器不断增加到无穷,我们就涉及了无穷重的希尔伯特空间的直积。无穷重和有限重直积空间有本质差别,序参量出现就源于此。
哥本哈根诠释还有一个会引起歧义的地方:波包塌缩与狭义相对论有表现上的冲突。例如,如图1,一个粒子在t =0 时刻局域在一个空间点A上,t =T 时测量其动量得到确定的动量p,则波包塌缩为动量本征态φ(x)~ exp(ipx) ,其空间分布在T 时刻后不再定域,整个空间均匀分布。因此,测量引起的波包塌缩导致了某种定域性的整体破坏:虽然B点在过A点的光锥之外(即A和B两点是类空的,通常不存在因果关系),但在t >T的时刻,我们仍有可能在B点发现粒子。按照狭义相对论,信号最多是以光的速度传播,而在瞬时的间隔发生的波包塌缩现象,意味着存在“概率意义”的超光速——T时刻测量粒子动量会导致体系以一定几率(通常很小很小) “ 超光速”地塌缩到不同的动量本征态上。这个例子表明,如果简单地相信波包塌缩是一个基本原理,会出现与狭义相对论矛盾的悖论。事实上,对于单一的测量,我们并不能确定地在B点发现粒子。因此,“事件”A和B的联系只是概率性的。而对于微观粒子而言,讨论经典意义下的因果关系和相关的非定域性问题,不是一个恰当的论题。概率性的“超光速”现象意味着,在概率中因果关系必须要仔细考量。
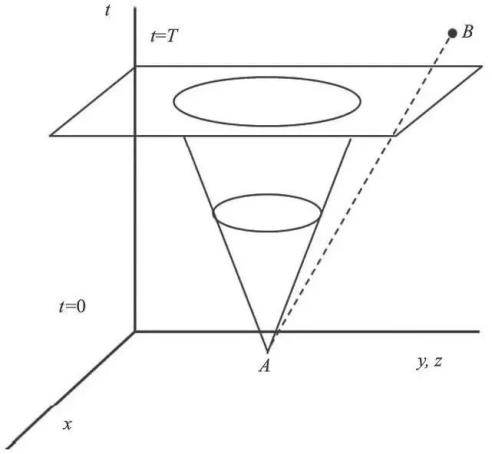
图1 四维时空中的整体波包塌缩:对定域态的动量测量,接受哥本哈根的观点,则会认为系统塌缩到动量本征态,从而可以出现在类空点上
综上所述,哥本哈根诠释带来概念困难的关键之处是广为大家质疑的第6 条“军规”——经典必要性或波包塌缩。量子力学的其他诠释,如多世界诠释、退相干诠释乃至隐变量理论,均是针对这一点,提出了或是在量子力学框架之内、或是超越之外的解决方案。
03
多世界诠释
对量子力学诠释采取“工具论(instrumentalism)”的态度,可以认为波函数不代表任何物理世界中的实体,也不描写实际的测量过程,而只是推断实验结果的数学工具。因此,在哥本哈根诠释中,波包塌缩与否,都不意味着实体塌缩,只是塌缩后可以据此推断重复测量的结果。虽然玻尔自己晚期也多次谈到这一点,但哥本哈根学派的思想并没有逻辑上的一致性。他们由此推及诠释量子力学必须借助经典世界,明显走向了本体论(ontology)的一面,经典世界是客观存在的本体。因此,从哲学意义上讲,哥本哈根诠释是一种二元论的混合体:微观世界由观察或意识决定,但实施观察的经典世界是客观存在的。
温伯格和盖尔曼(Murray Gell-Mann)等著名的理论物理学家,并不满足于哥本哈根诠释的绥靖主义和哲学上二元论的理解,他们从实在论(realism)立场出发,直到今天还在锲而不舍地追问波函数到底是什么、测量后变为什么。非常幸运,早在上一个世纪五十年代初,埃弗里特对这些基本问题给出了“实在论”或“本体论”式的回答——这就是相对态理论或后称多世界诠释。
量子力学的多世界诠释起源于休·埃弗里特(Hugh Everett)(图2)的博士论文。1957 年在《现代物理评论》发表了这个博士论文的简化版。发表文章的题目《量子力学的相对态表述》有些专业化,但科学上很准确。文章发表后被学界冷落多年,1960 年代末德维特(Bryce Seligman DeWitt)在研究量子宇宙学问题时,重新发现了这个“世界上保守好的秘密”,并把它重新命名为“多世界理论”。这个引人注目的名称复活了埃弗里特沉寂多年的观念,也引起了诸多新的误解和争论。

图2 休·埃弗里特(1930—1982):多世界诠释的创立者
埃弗里特提出多世界诠释之后,面对玻尔的冷落,不管他的老师惠勒(John Wheeler)如何沟通“多世界理论”和“标准”哥本哈根诠释、平滑它们的冲突,在答复《现代物理评论》编辑部的批评意见时,他还是挑明了他与哥本哈根诠释的根本分歧。他认为:“哥本哈根诠释的不完整性是无可救药的,因为它先验地依赖于经典物理……这是一个将‘真实’概念建立在宏观世界、否认微观世界真实性的哲学怪态。”这一点也是温伯格在尖锐批评哥本哈根诠释时所不断重复的要点、灵动之“蛇”的七寸。今天,不少人认为,多世界诠释的建立是使量子力学摆脱“怪态”走向正常态的基本理论。
多世界诠释认为,微观世界中的量子态是不能孤立存在的,它必须相对于它外部一切,包括仪器、观察者乃至环境中各种要素。因此,微观系统不同分支量子态|n> 也必须相对于仪器状态|Dn> ,观察者的状态|On> ……环境的状态|En> 来定义,从而,微观系统状态嵌入到一个所谓的世界波函数或称宇宙波函数(universal wavefunction):
(5)
它是所有分支波函数的叠加。埃弗里特等人认为,如果考虑全了整个世界的各个部分细节,Cn 可以对应于微正则系综Cn = 1/√N,N 是宇宙所有微观状态数。不必预先假设玻恩规则,通过粗粒化,可以证明|Cn|2 代表事件n 发生的概率。当然,这种处理取决于人们对概率起因的理解。
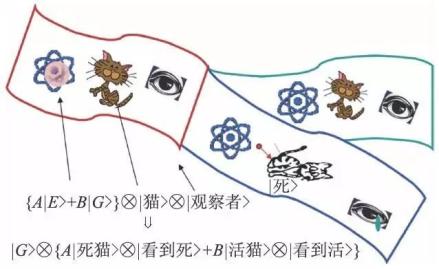
图3 薛定谔猫“佯谬”多世界图像:处在基态|0> 和激发态|1> 叠加态上的放射性核,通过某种装置与猫发生相互作用。处在|1> 态的核会辐射,触动某种装置杀死猫,而处在|0> 态的核不辐射,猫活着。这个相互作用结果使得世界处在两个分支上:在“死猫”的分支上,核辐射了,杀死了猫,观察者悲伤,也看到了这个结果,整个世界也为之动容;在“活猫”分支上,没有辐射,没有猫死,没有悲伤的观察者和悲切的世界。两个分支都存在,但观察者们不会互知彼此
多世界诠释认为,量子测量过程是相互作用导致了世界波函数的幺正演化过程,测量结果就存在于它的某一个分支之中。每一个分支都是“真实”存在,只是作为观察者“你”、“我”恰好处在那个分支中。薛定谔猫在死(活)态上,对应着放射性的核处在激发态|1> ( 基态|0> )上,这时观察者观测到了猫是死(活)的。我们写下猫态:
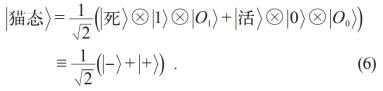
多世界诠释是说, 两个分支|-> =|死,1,O1> ≡ |死> ⊗ |1> ⊗ |O1> 和 |+> = |活,0,O0>≡ |活> ⊗ |0> ⊗ |O0> 都是真实存在的。测量得到某种结果,如猫还活着,只是因为观察者恰好处在|+> 这个分支中。
如果仅仅到此为止,人们会马上质疑多世界理论,并视之为形而上学:仅说碰巧观察者待在一个分支内,作为观察者的“你”、“我”在另一个分支里看到了不同的结果,观察者的“你”、“我”便“一分为二”了。人们显然不会接受这种荒诞的世界观。然而,埃弗里特、德维特利用不附加任何假设的量子力学理论,自洽地说明不同分支之间,不能交流任何信息。因此,在不同分支内,观察者“看到”的结果是唯一的。最近,本文作者及合作者通过明确定义什么是客观的量子测量,严格地证明了这个结论[37]。我们的研究进一步表明,埃弗里特的多世界诠释变成了一个犹如量子色动力学(QCD)一样正确的物理理论。QCD假设了夸克,但“实验观察”并没有直接看到夸克的存在。所幸QCD本身预言了渐进自由,它意味着夸克可能发生禁闭:两个夸克离得越近,它们相互作用越弱,反之在一定程度上,距离越远,相互作用越强,因而不存在自由夸克(当然,严格地讲,渐进自由是依据微扰QED证明的,而QCD 研究禁闭问题的本质可能是非微扰)。
多世界理论常常被误解为假设了世界的“分裂”、替代波包塌缩。事实上,埃弗里特从来没有做过这样的假设。多世界理论是在量子力学的基本框架(薛定谔方程或海森伯方程加上玻恩几率诠释)描述测量或观察,不附加任何假设。“分裂”只是理论中间产物的形象比喻。当初,埃弗里特投稿《现代物理评论》遭到了审稿人的严厉批评:测量导致的分支状态共存,意味着世界在多次“观测”中不断地分裂,但没有任何观察者在实际中感受到各个分支的共存。埃弗里特对这个问题的答辩也是思辨式的,但逻辑上很有说服力。他说,哥白尼的日心说预言了地球是运动的,但地球上的人的经验从来没有直接感觉到地球是运动的。不过,从日心说发展出来的完整理论——牛顿力学从相对运动的观点解释了地球上的人为什么会感觉到地球不动。理论本身可以解释理论预言与经验的表观矛盾,这一点正是成功理论的深邃和精妙所在。
今天看来,作为理论中间的要素,不自由的夸克和不可观测的世界分裂都是一样的“ 真实”,其关键是量子力学的多世界诠释能否自证“世界分裂”的不可观测性。由于世界波函数的描述原则上包含了所有的观察者,上帝也不可置身此外。因此,我们不再区分仪器、观察者或上帝,世界是否“分裂”问题于是就转化为观察或测量的客观性问题(Box 1):两个不同观察者观察的结果是否一致,观测结果之间是否互相验证一致。
事实上,为了证明多世界诠释中世界的分裂是不可观测的,埃弗里特首先明确什么是“观察”或“测量”。今天大家已经公认,测量是系统和仪器之间的经典关联,如果要求这种关联是理想的,对应于不同系统分支态的仪器态是正交的(完全可以区分)。如果观察者可以用另外的仪器去测量原来的仪器状态,得到相同的对应读数, 则两个仪器间形成理想的经典关联(Box 1)。
多世界诠释似乎完美地解决了哥本哈根诠释中面临的关键问题,但其自身仍然在逻辑上存在漏洞,这就是偏好基矢(preferred basis)问题。我们以自旋测量为例说明这个问题,设自旋1/2 体系世界波函数为
(7)
其中|U↑> (|U↓>) 代表相对于自旋态|↑> (|↓>) 的宇宙其他所有部分的态。按多世界论的观点,测得了自旋向上态|↑>,是因为它的相对态|U↑> = |D↑,O↑,⋯> 包含了指针向上的仪器D↑ ,看到这个现象观察者O↑ 以及相应的环境等。多世界诠释的要点是认为另外一个分支|U↓> =|D↓,O↓,⋯> 仍然是“真实”存在,但外在另一个(向上)分支中的观察者无法与这个分支进行通信,不能感受到向下分支的存在。然而,量子态|ϕ> 的表达式不唯一,即原来的世界波函数也可以表达为
(8)
其中新的基矢|±> = (|↑> ± |↓> )/√2 代表自旋向左或向右的态,而|U±> = (|U↑> ± |U↓> )/√2 代表系统与世界相对应的部分。很显然, |U±> 不会简单地写成仪器和观察者因子化形式,它不再是仪器、观察者和环境其他部分的简单乘积,测量的客观性不能得以保证。
上述考虑带来了所谓的偏好基矢问题:为什么对于同一个态,在谈论自旋取向测量时,我们采用了自旋向上和向下( |↑> 和|↓> )这种偏好,而非自旋左右。埃弗里特知道这个问题的存在,但他并不在意,他觉得任何测量都要有体现功能的仪器的特定设置,这种功能选择设置仪确定了偏好基矢。例如,在测量自旋的施特恩—盖拉赫实验中,我们通过选择非均匀外磁场的指向,来确定是测上下还是左右的自旋。然而,很多理论物理学家还是觉得多世界理论的确存在这样的不足。1981年祖莱克(Wojciech Zurek)把迪特尔·泽(Dieter Zeh)1970年提出的量子退相干观念应用到量子测量或多世界理论,为解决偏好基矢问题开辟了一个新的研究方向。
04
量子退相干诠释或理论
提出量子退相干观念的目标之一是要解决所谓的“薛定谔猫佯谬”,即为什么常态下宏观物体不会展现量子相干性。大家知道,接着波粒二象性的观点,任何实物粒子可以表现出波动行为,可以发生低能物体穿透势垒的量子隧道效应。关于微观体系,电子、原子、中子、准粒子(库珀对)乃至C60这样的大分子,实验上已经展示了量子隧道效应,并在实际技术中得到了广泛应用,如STM(扫描隧道显微镜)。现在的问题是一个宏观物体,像足球、人、崂山道士,可否发生量子隧道效应?崂山道士可否破墙而出,破墙而入?初步的看法是,这是不可能的,因为宏观物体的质量较大,物质波波长短,必远远小于物体的尺度,不可能展示出量子相干效应。
迪特尔·泽和他的学生埃里希·朱斯(Erich Joos)(图4)从另一个角度给出了相同的答案:一个宏观物体必定和外部环境相互作用,即使组成环境的单个微粒很小,与宏观物理碰撞时能量交换可以忽略不计,环境也可以记录宏观物体运动信息,从而与宏观物体形成量子纠缠,发生量子退相干。此时,环境的作用相当于在系统不同基矢态中引入随机的相对相位,平均结果使得干涉项消失。因此,不同的(动量)态之间的相干叠加不存在了。

图4 量子退相干理论创立者迪特尔·泽(左图,http://www.ijqf.org/members-2/dieter/)和他的学生埃里希·朱斯(右图)
量子退相干理论最近已引起物理学界极度重视,一个重要原因是量子通讯和量子计算研究的兴起。量子计算利用量子相干性——量子并行和量子纠缠以增强计算能力,而退相干对其物理实现造成了巨大障碍。当年迪特尔·泽提出量子退相干的概念时只是一位讲师,他的文章不能在知名的学术刊物上发表,创新的观点受到著名学者尖酸的批评,整个70年代这个重要工作被物理学家系统性忽视,几乎影响了迪特尔·泽后来的学术职业生涯。后来,退相干理论渡过1980年代这个黑暗期,祖莱克加入量子退相干研究队伍。他的着眼点是解决偏好基矢问题,并为量子测量问题的探索提供了新的思路。
在量子退相干理论中, 处在初态|φS> =ΣCn |n> 的系统与处在初态|E> 上的环境发生非破坏(不交换能量)的相互作用,使得t 时刻总的状态变为
(9)
这里|En(t)> =Un(t)|E> ,而Un = exp(-iHnt )是非破坏相互作用V =Σ|n>
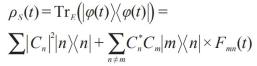
一般包含非对角项,其中Fmn =
(11)
这时,描述大系统量子态的量子相干叠加态|φS>变成了没有量子相干的密度矩阵,实现了从量子叠加态到经典几率描述的转变。这相当于实空间中干涉条纹消逝(Box2)。
我们的研究证明,即使宏观物体与外界完全隔离,内部自由度与质心运动自由度的耦合也会引起退相干,特别是当环境是由很多粒子组成,则可能有因子化的末态,它给出退相干因子。由于,当N → ∞, F01 → 0,这个发现原则上解决了薛定谔猫佯谬。只许把“ 死” 与“活”当成质心自由度的状态,完整的猫态应当写为
(12)
则猫的密度矩阵的非对角项|死>
<活|将伴随着退相干因子。显然,宏观猫的干涉项正比于fdl ,在宏观极限下, n → ∞ , fdl="0" ,从而干涉效应消逝。< p>针对各种实际中的宏观粒子,迪特尔·泽和他的学生埃里希·朱斯在1985 年仔细地计算了它们在各种环境中空间运动的退相干因子。他们得到一般的系统约化的密度矩阵:
(13)
其中局域化因子
(14)
决定于环境粒子在宏观物体上的有效散射界面σeff 。表1给出了各种物体局域化因子的列表。
表1 各种物体的局域化因子
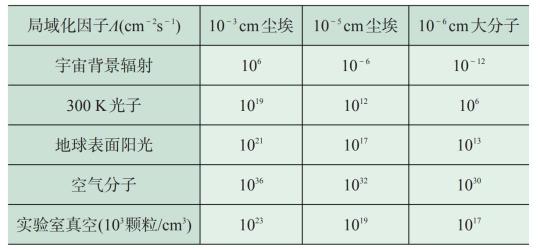
总之,作为客观物体象征的薛定谔猫或仪器的运动,可分为集体运动模式和内部相对运动模式,它们之间存在某种形式的信息交换,但不交换能量,由于这种特殊形式的耦合,形成集体运动模式和内部相对运动模式的量子纠缠,内部运动模式提供了一种宏观环境。如果观察者只关心集体运动而不关心内部细节,集体运动就会发生量子退相干,薛定谔猫佯谬也就不存在了。
我们最近发现,薛定谔猫的退相干还有一个内禀的原因,这就是相对论效应:一群自由粒子,其能量最低阶非相对论效应正比于p4,它使得质心自由度与内部自由度内禀地耦合起来,产生薛定谔猫的内禀退相干。这个发现进一步表明,“月亮”在没有人看它的时候,仍然是客观存在的。这是因为“月亮”是一个宏观物体,人类的“看”必定忽略了“月亮”的内部细节。由于相对论效应,内部环境与“看到”的宏观自由度有天然的耦合,使得退相干无处不在!
以上的分析可以正面回答目前热炒的“量子意识”问题。我们认为,把至今备受质疑的哥本哈根诠释的波包塌缩假设作为论证基础,大谈量子意识,科学知识非常之不准确!虽然现在的物理理论还不能完全解释意识,但也绝不能断言它与量子有直接关系。因为意识必源自人这样的常态宏观物体,后者注定退相干。把量子力学和意识这种高级生命独有的现象联系起来并没有为理解意识的产生与存在提供任何高于猜测的理解。其实,物理学解释不了的问题就不应该牵强附会地解释。要承认科学的定位和局限性,有些问题不在目前科学研究范畴内,非要披上科学的外衣就是对科学的侵犯。
1981 年,祖莱克(图5)把迪特尔·泽的量子退相干理论应用到冯·诺依曼量子测量理论,把测量过程看成系统S与测量仪器D相互作用产生经典关联的一种动力学过程。在冯·诺依曼量子测量中,通过与环境作用,系统+仪器形成的复合系统进一步与环境量子纠缠:
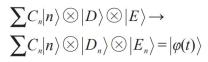
(15)
从而有复合系统的约化密度矩阵变为
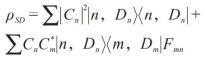
(16)
现在,相互作用只是产生系统态|n> 与仪器态|Dn >的量子纠缠,并非纯概率性的关联。当其中退相干因子Fmn =

需要强调的是,应用于量子测量问题,退相干理论必须能够解释指针态(pointer state)的衍生(emergence)。这个概念与多世界理论中相对态的观念是一致的。如上所述,环境作用选择仪器+系统的特定基矢进行退相干,而密度矩阵的对角元和非对角元则在不同的坐标变换下是相对的。如果采用另一组基矢|n′> =ΣSnn′+|n>,则有非对角项|n′>< m′| 的存在。正是由于这种基矢的相对性,量子纠缠无法直接描述量子测量,这就是所谓的偏好基矢问题。
在整个宇宙(系统+仪器+外部环境)的时间演化过程中,因子化的宇宙初态会变成一个针对被测基矢的相对态,相对态中每一项的系数恰好是初态中系统相干叠加态中的系数。这时,我们说相对系统态而言,仪器态是一个指针态,而环境所充当的角色是诱导了一个超选择定则(称为eniselection),选择了这样特定的基矢。退相干理论的第二个要点是初态因子化的假设。它隐含的意思是,没发生相互作用之前,系统的相干叠加态是独立于测量仪器和环境而存在的。以后,相互作用使得世界波函数保持一种准因子化的形式,即形成具有和系统初态系数一样的施密特系数的相对态。这个假设可以有一个逻辑上的改进。因为因子化形式依赖于张量积定义,其不唯一性使退相干理论进一步也遭遇到质疑的逻辑障碍。也许这与偏好基矢问题是等价的。在更完美的理论中,应该事先不假定因子化的形式,让环境诱导出来的时间演化产生相对态的系数,实现完全客观的量子测量过程。但是,这种处理遇到的关键问题是怎样把这个理论结果与依赖于初态的实验相比较。
05
量子自洽历史、量子达尔文和各种诠释的统一
量子退相干理论强调的是环境引起的量子退相干,但对于整个宇宙而言,谈其环境是没有意义的,宇宙本质是个孤立体系。如果有朝一日人们完成了引力量子化,没有环境影响,经典引力如何出现?没有经典引力,我们如何理解苹果落地和月球绕日而行、如何描述整个宇宙在经典引力作用下的演化?因此,为了描述量子宇宙的所有物理过程,我们的确需要一个更加普遍的量子力学诠释:这里没有外部测量,也没有外部环境,一切都在宇宙内部衍生,在宇宙内部也可以看到一个从量子化宇宙约化出来的经典世界,经典引力支配着各种各样的物理现象。针对这个问题,基于格里菲斯(Robert Griffiths)和欧内斯(Roland Omnes)等人提出自洽历史处理(consistent history approach),哈特尔(James B. Hartle)和盖尔曼等人发展了退相干历史的量子力学诠释。
量子力学自洽历史诠释是格里菲斯(图6)在1983 年提出来的。与多世界诠释一样,量子力学自洽历史诠释也是从世界波函数出发,它强调的“历史”是有测量介入的离散时间演化序列。如图7,我们用一个描述测量结果的投影算符序列
(17)
来定义量子世界包含时间演化和测量的历史。Pj代表在t =j 时到某本征态上的投影。不同的历史,相当于多世界理论中世界分裂的不同分支。显然,任意给定一个历史的集合,不同的历史之间有干涉效应,每一个历史相互不“独立”,不能定义经典几率。为了衍生出经典概率,格里菲斯对描述历史的投影算符乘积给出了自洽条件Tr( HjρHl ) = 0( j ≠ l) ,其中ρ 代表系统的密度矩阵。满足这个条件的历史集合中的历史被称为自洽的历史。对每一组自洽的历史,可以赋予一个经典概率描述:Pr(j) = Tr( HjρHj ) 。如果把每一个历史当成多世界理论中世界波函数时间域上的一个分支,自洽历史处理可以视为多世界理论的某种推广发展。在这个意义下,多世界可以看成是我们唯一宇宙“多种选择的历史”。按美国加州理工学院的哈特尔和盖尔曼的观点,虽然世界只有一个,但却可以经历很多个可能历史组。

图6 自洽历史诠释的创立者格里菲斯(Robert Griffiths,孙昌璞2005 年摄影)
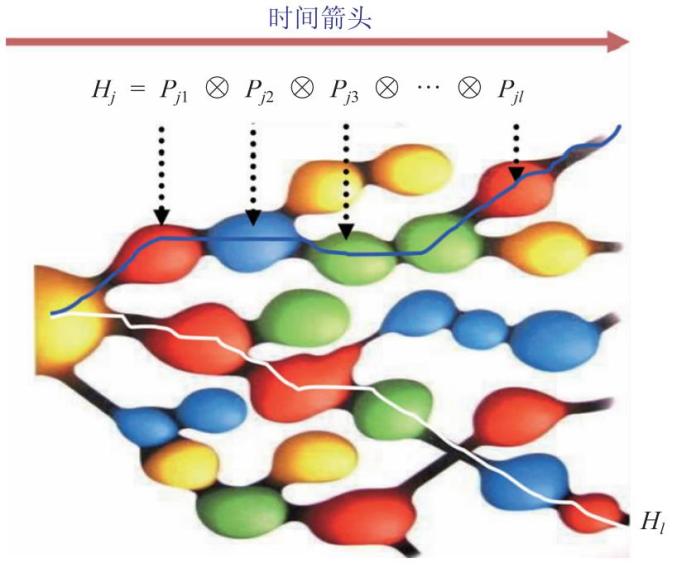
图7 自洽历史诠释与多世界理论的相似性:“世界只有一个,历史是多重的”
下面以薛定谔猫佯谬为例,简要地告诉大家什么是自洽历史描述:如果我们能够测量每一个时刻组成猫的所有粒子的坐标,不同时刻的位置测量构成了系统的精(细)粒化的历史。不同时刻的位置投影算子乘积构成历史的描述,其中
(18)
指标j 代表组成猫的不同粒子。Hi =H(t = 0,1,⋯,T ) 描述了粒子的轨迹,不同Hi可能会不“独立”,这样历史通常是不自洽的。我们猜想,对于薛定谔猫而言,描述质心运动的那些投影Hi,忽略量子涨落,艾伦菲斯特方程退化成牛顿方程,形成一组自洽的历史,然后赋予经典意义上的几率。我们猜想,只对应轨迹退相干的投影乘积序列,才可以确定地构成自洽的历史。因此,自洽历史诠释的坐标表示本质上是退相干历史诠释。
哈特尔和盖尔曼等人发现,带有测量的历史序列可以用路径积分表达。针对量子引力和宇宙学,提出今称为退相干历史的量子力学诠释:宇宙体系演化过程粗粒化抹除若干可观察对象类之间的量子相干性,经典几率可以自洽地赋予每一个可能的路径。事实上,对任何瞬间宇宙中发生的事件作精确化的描述,构成了一个完全精粒化历史(completely fine-grained history)。不同精粒化的历史之间是相互干涉的,不能用独立的经典概率加以描述。但是,由于宇宙内部的观察者能力的局限性或需求的不同,只能用简化的图像描述宇宙(如只用粒子的质心动量和坐标刻画粒子的运动),本质上是对大量精粒化历史进行分类的粗粒化(coarse-grained)描述。粗粒类内的相位无规可以抹除各类粗粒化历史之间的相干性,从而使得粗粒化的历史形成所谓退相干的历史(decoherence history)。通过这种退相干历史的描述,原则上对量子引力到经典引力的约化给出了自恰的描述。
我们还可以借助“薛定谔猫”来展示什么是退相干历史诠释。假设“猫”作为一个宏观物体是由大量有空间自由度的粒子组成,每一个粒子有自己空间运动的轨迹,满足各自的薛定谔方程,它们每一个的演化构成了“猫”的精粒化的历史,代表了“猫”的动力学所有的微观态细节。如果用路径积分描述这些“历史”,则不同路径之间是干涉的。由于这些粒子间存在相互作用,则“精粒化历史”对应的“轨道”与自由粒子的轨道不是一一对应的。现在我们不关心组成“猫”的每一个粒子的运动细节,只关心它的质心或者其他宏观自由度。某个特定宏观自由度的运动是微观自由度某种集体合作的结果,可以视为“猫”的所有微观演化过程的粗粒化。由于相对运动的影响,它的相干叠加态的时间演化会导致相位差的不确定性,从而相干性消逝。如图8所示,从路径积分的观点看,粗粒化后两条不同路径是不相干的,相干函数变为零,从而导致所谓退相干的历史。
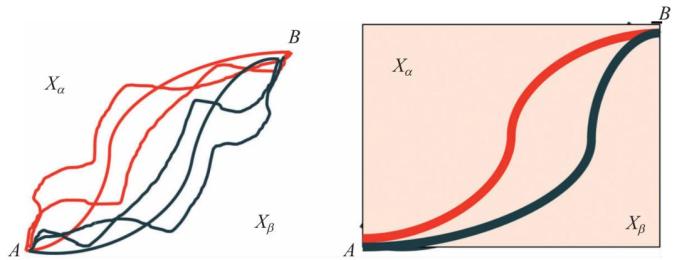
图8 粗粒化导致观察结果的量子退相干:从轨道到轨道类的路径积分
不管退相干历史也好,自洽历史也好,仍然存在偏好基矢的取向问题。同一个世界,有不同组合的自洽历史集,选择哪一个,有观察者或者“你”、“我”的偏好。祖莱克提出了量子达尔文的观点去解决这个问题。量子达尔文主义认为,“微观量子系统是可测量的”这一经典属性是由宏观外部环境决定的,只有那些在环境中能够稳定(robust)保持的性质才是微观系统的真正属性。只有那些在环境中残存下来的属性才是客观的,因为它不取决于个别人的意识,而是取决于它以外包括许多观察者的整个环境,这一点很像多世界的相对态。在量子达尔文的诠释中,环境的作用不再仅仅只是一个产生噪音的破坏者,它本质上还是一个有足够信息冗余度的记录器和见证者。如果把环境分成几个子系统,把其中的一个或几个用来记录系统信息,其他的则用来比对是否记录到相同的信息。如果不同的部分都记录了相同的东西,则这是一个微观系统固有、可在经典世界展现的东西,只有这样的属性才是客观的。
从这个意义上讲,这样的宏观环境与系统耦合,虽然可以不转换能量,但可以记录信息,使得系统“进化”(演化)到一个经典的状态——用非对角项消逝的退相干密度矩阵表示,使之对角化的基矢就是所谓的偏好基矢。如果把环境分成几个子系统,当作不同的观察者,则不同观察者得到了相同的观察结果。我们以两个观察者测量自旋为例,说明量子达尔文的观念。包含一个系统和两个观察者(O1和O2)的世界波函数可以写为
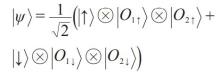
(19)
如前所述,当两个观察者态是正交的,则O1和O2对于基矢|↑> 和|↓> 得到相同的结果,而对另外基矢|+> 和|-> 则不然。量子达尔文的要点在于上述世界波函数是O2与系统间特定相互作用导致的稳态结果——一种“自然选择”。从数学表达式看,这个表述与多世界诠释是等价的,只是强调了环境记录信息的冗余性。当然,多世界理论强调了要考虑|↑> ( |↓> )以外的所有世界的态。它虽然没有明确环境对基矢的客观选择,但暗含了信息冗余的要求。
06
结束语
为解决哥本哈根诠释二元论的逻辑困境和物理悖论,过去人们提出了各种各样量子力学诠释。从本文讨论可以看出,它们的核心思想本质上来自于逻辑简练、物理寓意深远的、但图像十分反直觉的多世界诠释。多世界理论表达的是“一个波函数,多个世界”,而由它发展出来的自洽历史诠释讲的是“一个世界,多个历史”。
我们注意到,由于媒体和初级科普的不正确解释、以讹传讹,加上一些“知名”学者的不读原文、不求甚解(或不读书好求甚解),多世界诠释被污名化了许久。特别是目前不少人觉得哥本哈根诠释的正确是天经地义的,而多世界诠释则被认为是形而上学的甚至是伪科学。当然,如果不把波函数看成是本体论的东西,而只是从工具主义的角度把它看成是一个预测实验结果的数学工具,波包塌缩的预言和多世界诠释或量子退相干描述一般没有差别。但是,量子力学的哥本哈根诠释强调必须借助经典世界,从逻辑上讲是不自洽的。从哲学角度讲,量子力学的哥本哈根版本是一种二元论,而一个理想的完美的理论应该是一元论:一切源于量子,经典只是量子体系宏观极限下的“衍生”现象。
诺贝尔奖获得者塞尔日·阿罗什(Serge Haroche)认为[39]:“实验室中的测量远不是教科书中的投影假设” (“Most measurements are far from obeying the textbook projection postulate”)。既然测量是一个相互作用导致的幺正演化,要形成一个理想的仪器与被测系统的量子纠缠,需要一定的时间。当测量仪器变得足够宏观,这个时间会变得无穷之短,这个过程就是所谓的渐进退相干过程[40]。阿罗什在精心设计的腔量子电动力学实验中观察到了有演化时间表征的单个体系的渐进退相干过程。到底是哥本哈根诠释的投影测量还是与“多世界”有关的幺正演化测量,我们有可能根据测量时间效应在实验上加以区分。因此,量子力学诠释问题之争绝不是在讨论“针尖上的天使”。
量子芝诺效应的实验验证曾经被人看成对波包塌缩的证实。过去的十多年,我们曾经针对量子芝诺效应根源系统地探讨了量子力学诠释问题[41-43]。我们先是针对两个已有的、用波包塌缩诠释的实验给出了无需波包塌缩的动力学解释,进而设计了核磁共振测量系统[44],实现了有别于波包塌缩的量子测量。实验的确展示了测量时间的效应。最近,美国圣特路易斯小组利用超导量子比特系统又一次验证了我们的这种想法[45]。这些结果表明,解释量子力学现象并非一定需要哥本哈根的波包塌缩诠释!依据并无共识的哥本哈根诠释、不加甄别地发展依赖诠释的量子技术,在量子技术发展中会导致技术科学基础方面的问题。随着时间的推移,这种问题严重性会逐渐凸显出来。显然,如果不能正确地理解量子力学波函数如何描述测量,就会得到“客观世界很有可能并不存在”的荒诞结论;如果有人不断宣称“实现”了某项量子技术的创新,但何为“实现”却依赖于有争议的、基于波包塌缩的“后选择性”,这样的技术创新的可靠性必定存疑。因此,澄清量子力学诠释概念不仅可以解决科学认识上的问题,而且可以防止量子技术发展误入歧途。
致谢 感谢中国人民大学张芃教授、中国工程物理研究院研究生院傅立斌研究员、北京理工大学徐大智副教授,以及课题组成员戴越博士、董国慧和马宇翰对本文提出的批评和建议。感谢张慧琴博士在文字方面不胜其烦的协助和修改。
Box1:“世界分裂”的不可观察(测量)性
我们先假设观察者O通过仪器D测量系统S。三者的相互作用导致系统演化到一个我们称之为世界波函数的纠缠态:
在每一个分支
中, {|S>} 是系统的完备的基矢, {|dS>} 和{|OS>} 分别是与系统基矢|S> 相对应的仪器和观察者的态基矢。为了简单起见,一般情况下|OS> 可以代表系统和仪器以外世界所有部分,包括观察者和整个环境,通常不预先要求它们是正交的。
由于O是宏观的,则它对量子态反映是敏感的,有S|OS′> = δSS′[38]。平均掉环境作用,系统和仪器之间形成一个经典关联,
进而,如果仪器态是正交的,S|dS′> = δSS′ ,则ρSD 代表一种理想的经典关联。这时,如果观测的对象是系统的力学量A, |S> 是它的本征态, A|S> = aS|S> ,则系统本征态是正交的,从而仪器和观察者之间也形成理想的经典关联:
这表明,观察者O在仪器D上读出了S,且对于aS的几率为|CS|2 。
以上分析表明,观察者O用仪器D测量系统S 的(厄米)力学量A,理想的测量要求三体相互作用导致的纠缠态|φ> 是一个GHZ 型态,即 {|dS>} 和{|OS>} 是两个正交集。这时,观察者和系统之间也会形成一个系数相同的理想经典关联态,
因而我们说测量是客观的,这里可以把仪器和观察者当做两个不同的观察者,不同的观察者看到相同的结果。
现在我们假设仪器的状态 |dS>不是正交的,则|dS>可以用正交基|DS> (B|DS> = dS|DS>) 展开:
其中, CSS′=S′|dS> 。这时
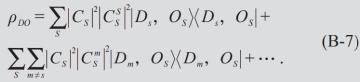
这表明|S> 分支中的观察者有一定的几率看到了另一个分支中仪器的读数——分支态|Dm> ,观察到了“分裂”!因此,要求理想测量( |φ> 是理想的GHZ态),则我们观测不到分裂。
我们还可以用反证法说明世界分裂是不可观察的。设世界波函数为
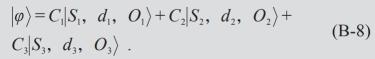
当|O1> = |O2> ,观察者O不能区分|S1> 和|S2> ,因此看到了世界的分裂,或
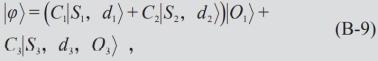
代表着观察者O看到世界分裂,因为它不能区分|S1> 和|S2> 。这时,
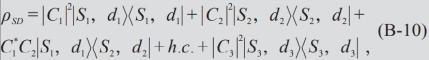
非对角项的存在意味着仪器和系统之间不能形成很好的经典关联。
Box 2:量子干涉与量子退相干
为了考察量子相干性与通常量子干涉之间的关系,我们在坐标表象{φ(x) =,φn(x) =} 中写下密度分布:
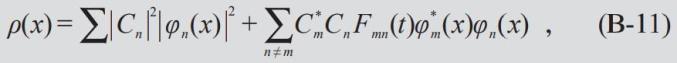
其中ρd(x) =Σ|Cn|2 |φn(x)|2代表强度相加项, 而Σn≠mCm*CnFmn(t)φm*(x)φn(x) 代表相干条纹,当Fmn(t) = 0 相干条纹消逝。
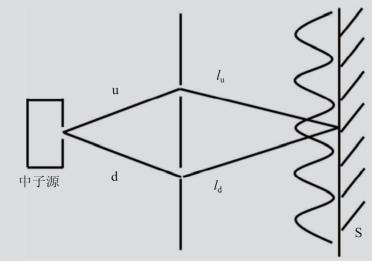
我们从双缝实验可以进一步形象地说明这一点。由中子源出射的中子束经双缝在屏S上干涉。
遮蔽上( 下) 缝的波函数|0> (|1>) 的坐标表示为
φu(x) =∝ eikx (φd(x) =∝ eik(x + Δ) ), 其中Δ = ld - lu是“光程差”。于是, |φ> ∝ |0> + |1> 给出约化密度矩阵:
当0| E1> = 1 ,则ρ(x)∝ cos Δk ,否则ρ(x) = 常数,无干涉条纹。
综上所述,环境的存在就像一个观察者在不断地监视着系统的运动,它通过与系统纠缠引入了等效的随机相位Δθ , 状态|φ(0)> = |0> + |1> , 被测后变为|φ′> = |0> + eiΔθ |1> ,平均结果给出:
其中,随机相位Δθ 是由等效相位因子eiΔθ 的平均值iΔθ> =0| E1> 来定义。当它趋近于零,干涉条纹消逝,即退相干发生。
参考文献
[1] Jammer M,Merzbacher E. The Conceptual Development of Quantum Mechanics. New York:McGraw-Hill,1966
[2] 孙昌璞. 物理,2000,29(08):457
[3] 孙昌璞,衣学喜,周端陆 等. 量子退相干问题. 见:曾谨言,裴寿镛 主编. 量子力学新进展(第一辑). 北京:北京大学出版社,2000
[4] 孙昌璞. 物理,2001,30(05):310
[5] Jammer M. The Philosophy of Quantum Mechanics. New York:John Wiley& Sons,1974
[6] 何祚庥. 物理,1993,22(7):419
[7] 孙昌璞,全海涛. 物理,2013,42(11):756
[8] 汪克林,曹则贤. 物理,2014,43(6):381
[9] Mermin N D. Physics Today,2004,57 (5):10
[10] 格里宾 著. 匡志强 译. 量子、猫与罗曼史(薛定谔传). 上海:上海科技教育出版社,2013. 译本见:Gribbin J. Erwin Schrodinger and the Quantum Revolution. London: Bantam Press,2012 [11] Weinberg S. Physics Today,2005,58:11,31
[12] Weinberg S. Lectures on Quantum Mechanics (2nd Edition). New York:Cambridge University Press,2015
[13] 温伯格. http://www.huanqiukexue.com/a/qianyan/tianwen__wuli/2016/1123/26804.html
[14] Everett H.Reviews of Modern Physics,1957,29(3):454
[15] DeWitt B S,Graham N. The Many Worlds Interpretation of Quantum Mechanics. Princeton:Princeton University Press,1973
[16] Ollivier H,Poulin D,Zurek W H. Physical Review Letters, 2004,93(22):220401
[17] Tipler F J. Proceedings of the National Academy of Sciences, 2014,111(31):11281
[18] Byrne P. The Many Worlds of Hugh Everett III: Multiple Universes,Mutual Assured Destruction,and the Meltdown of a Nuclear Family. New York:Oxford University Press,2010 [19] Lehner C. The Everett Interpretation of Quantum Mechanics: Collected Works 1955-1980 with Commentary. Princeton:Princeton University Press,2012
[20] Northey M,Mckibbin J. Many Worlds ?:Everett,Quantum Theory,& Reality (Reprint Edition). New York:Oxford University Press,2012
[21] Wallace D. The Emergent Multiverse: Quantum Theory according to the Everett Interpretation (Reprint Edition). New York:Oxford University Press,2014
[22] Bohm D. Physical Review,1952,85(2):166
[23] Bohm D. Physical Review,1952,85(2):180
[24] Zeh H D. Foundations of Physics,1970,1(1):69
[25] Joos E,Zeh H D. Zeitschrift Für Physik B Condensed Matter, 1985,59(2):223
[26] Joos E,Zeh H D,Kiefer C et al. Decoherence and the Appearance of a Classical World in Quantum Theory. Berlin:Springer-Verlag,2003
[27] Zurek W H. Reviews of Modern Physics,2003,75(3):715
[28] Zurek W H. Physical Review D,1981,24(6):1516
[29] Griffiths R B. Journal of Statistical Physics,1984,36(1-2):219
[30] Griffiths R B. Consistent Quantum Theory. New York:Cambridge University Press,2003 [31] Gell-Mann M,Hartle J B. Quantum Mechanics in the Light of Quantum Cosmology. In:Complexity,Entropy,and the Physics of Information. ed. Zurek W. Reading: Addison-Wesley,1990
[32] Gell-Mann M,Hartle J B. Physical Review D,1993,47(8):3345
[33] VonNeumann J. Mathematical Foundations of Quantum Mechanics. Princeton:Princeton University Press,1955
[34] Peres A. Quantum Theory:Concepts and Methods. Dordrecht:Kluwer Academic Publishers,1995
[35] 赫尔奇·克劳 著. 肖明,龙芸,刘丹 译. 狄拉克:科学和人生. 长沙:湖南科学技术出版社,2009
[36] Wigner E P. Remarks on the Mind-Body Question. ed. Good I J. In:The Scientist Speculates. London:Heinemann,1961
[37] Li S W,Cai C Y,Liu X F et al. Objectivity of quantum measurement in many-observer world. arXiv:1508.01489,2015
[38] Quan H T,Song Z,Liu X F et al. Physical Review Letters, 2006,96:140604
[39] Haroche S,Raimond J M. Exploring the Quantum:Atoms,Cavities,and Photons. New York:Oxford University Press,2006
[40] Brune M,Hagley E,Dreyer J et al. Physical Review Letters, 1996,77:4887
[41] Sun C P. Physical Review A,1993,48(2):898;评述文章见:Sun C P,Yi X X,Liu X J. Fortschritte der Physik-Progress of Physics,1995,43:585
[42] Xu D Z,Ai Q,Sun C P. Physical Review A,2011,83:022107
[43] Ai Q,Xu D Z,Yi S et al. Scientific Reports,2013,3:1752
[44] Zheng W Q,Xu D Z,Peng X H et al. Physical Review A,2013, 87:032112
[45] Harrington P M,Monroe J T,Murch K W. Physical Review Letters,2017,118:240401
END

更多精彩文章请点击下面“蓝字”标题查看:
对麦克斯韦方程组拓展的评论王青教授:深入理解“拓展的麦克斯韦方程组”——2.0版王青教授:理解王中林院士“拓展的麦克斯韦方程组”“碰瓷”麦克斯韦:伽利略协变和洛伦兹协变电磁场论趣谈热点:运动介质洛伦兹协变电磁理论2021年《物理与工程》优秀论文、优秀审稿专家、优秀青年学者名单王青教授:源自苏格拉底的问题驱动式教育——在互动中共同学习和成长读后感:教育中的现实和远方王青教授:昨晚(6月9日),清华电动力学期末考试朱邦芬院士:“减负”误区及我国科学教育面临的挑战《物理与工程》2022年第1期目录乐永康:新冠肺炎疫情防控下美国物理实验教学及中美情况对比顾牡:对于重新制定的《非物理类理工学科大学物理课程教学基本要求》的认识和体会朱邦芬院士:从基础科学班到清华学堂物理班朱邦芬院士:对培养一流拔尖创新人才的思考李学潜教授:物理是一种文化李学潜教授:如何帮助物理系学生迈过从高三到大一这个坎穆良柱:物理课程思政教育的核心是科学认知能力培养穆良柱:什么是物理及物理文化?穆良柱:什么是ETA物理认知模型穆良柱:什么是ETA物理教学法吴国祯教授:我的国外研究生经历印象——应清华大学物理系“基科班20年·学堂班10年纪念活动”而写
陈佳洱,赵凯华,王殖东:面向21世纪,急待重建我国的工科物理教育王亚愚教授:清华物理系本科人才培养理念与实践葛惟昆教授:关于中外人才培养的几点思考安宇教授:为什么传统的课堂讲授模式需要改变安宇教授:其实教学就是积累的过程刘玉鑫教授:关于本科生物理基础课程教学和教材编著的一些思考沈乾若:重创理科教育的美加课程改革Henderson C:美国研究基金支持下的物理教育研究及其对高等物理教育的影响《物理与工程》期刊是专注于物理教育教学研究的学术期刊,是中国科技核心期刊,1981年创刊,欢迎踊跃投稿,期刊投审稿采编平台:
http://gkwl.cbpt.cnki.net
欢迎关注
《物理与工程》微信公众号
原标题:《量子力学诠释问题》

