蝴蝶效应和混沌故事
原创 陈关荣 集智俱乐部

导语
“人们经常都会看到,纯粹理论研究的一点点成果,也许在很长时间之后,会导致连做该纯理论研究的科学家都始料不及的实际应用。”
——爱德华·诺顿·洛伦茨
陈关荣 | 作者
邓一雪 | 编辑

他不是文学家,却在不经意间留下了一个脍炙人口的新成语:蝴蝶效应。
他是麻省理工学院(MIT)气象系已故教授爱德华·诺顿·洛伦茨(Edward Norton Lorenz,1917年5月23日-2008年4月16日)。

Edward Norton Lorenz
洛伦茨是一位气象学家,研究大气物理,曾孜孜不倦地去探索多年来被学术界认为“算不上是科学” (“less than science”)的“长期天气预报”。气象学家甚至普通人都知道,长期天气预报是不精确的:谁知道明年的今天这个地区的天气会怎么样呢?洛伦茨的伟大贡献之一,是以一个简单具体的物理学模型及其数学原理向世人示明:精确的长期天气预报的确是不可能的。
洛伦茨很早就注意到,虽然一年有四季,但准确地说气候和天气都没有严格的周期规律。在1950年代,他尝试建立一个数学模型来描述大气层上下温差引起气流变化的动力学过程。在作了许多简化之后,他构建了一个12个变量的非常复杂的微分方程组。可是,在当年没有高速计算机辅助的条件下,谁都没有办法对之进行分析和计算。洛伦茨试图进一步简化这个数学模型,但直觉上认为需要保留偶数个方程才能准确地描述气流动态,多次尝试之后以失败而告终。
1961年的一天,他和同在“MIT一般环流研究项目”工作而后来成为“现代气候理论之父”的巴里·萨尔茨曼(Barry Saltzman)教授一起探讨了他的模型简化问题。那时萨尔茨曼正在研究非线性Benard对流,通过谱展开得到了7个变量的降阶非线性方程组。萨尔茨曼告诉洛伦茨,说他得到了一些周期解,但也有不稳定的解。洛伦茨仔细观察了那些结果,发现7个变量中的4个周期解很快衰减从而变得不重要了,而其他3个则会保持长时间的非周期性变化。洛伦茨非常感激萨尔茨曼的实验结果给他提供的启示,感觉到类似这样的3个变量方程组应该足以用来描述他所期望的气流运动的非周期性。果然,他将自己的模型作了相应的简化后,仅保留了3个变量,发现能够观察到非周期性动力学现象。
当年洛伦茨求解这3个变量的方程组用的是一台Royal McBee LGP-30计算机,放置在MIT第24号楼第五层。这台机器比书桌还大,重约260公斤,可是速度极其缓慢,连今天的笔记本电脑都比它快上一百万倍。当年,计算机程序是由两位年轻女助手艾伦·费特(Ellen Fetter)和玛格丽特·哈密顿(Margaret Hamilton)负责编写的。艾伦和玛格丽特分别从Mount Holyoke College和Earlham College 数学专业本科毕业,两人来到洛伦茨实验室工作后才开始学习编写计算机程序。不过她俩都很称职。特别值得一提的是那位哈密顿女士,聪明的她很快就成为一位编程能手。她离开MIT比较早,后来加盟国家宇航局(NASA),先后为登月飞船编写控制程序和为空中试验室(Skylab)编写操作软件,2003年获NASA授予航天杰出贡献奖(Exceptional Space Act Award),2016年荣膺美国总统自由勋章(Presidential Medal of Freedom),2017年还被乐高(LEGO)游戏产品选定为成功女士偶像人物。

Royal McBee LGP-30计算机
现在回来继续说洛伦茨的故事。
故事发生的这一天是周五,洛伦茨如常来到了办公室,继续用他推导出来的简化数学方程组做天气预报仿真。他计划把昨天的仿真重复一遍,以保证计算结果准确无误。他知道那台蜗牛机器运算极慢,需要一个多小时才能完成计算,便踱进了学院旁边的小咖啡馆。喝完咖啡回到办公室后,他一看仿真结果大吃一惊,发现新画出来的曲线与昨天的记录大相径庭:两条曲线从相同的初始点出发,在起初几周时间点上的预报相互吻合得很好,但随后两者迅速分离,大约两个月后便变得毫不相关了。他反复检查了公式,两位女士也反复检查了程序,都没有发现任何错误。这让他百思莫解。
经过反复核查,在排除了计算机故障的可能性之后,他注意到了两次仿真试验过程之间的一个微小差异。当时的计算机运算精确度是保留小数点后6位数字的,因此他在第一次计算中输入了初始值0.506127。但在第二次计算中,他图省事输入了0.506,觉得这不到千分之一的“四舍五入”不会带来什么影响。现在他发现自己错了,这影响其实大得很。
历史上许多重大机遇都出现在这种毫不显眼的事情和毫不惊人的时刻:0.506不够精确么?改为0.506127再算一遍就好了嘛,还来得及去多喝杯咖啡呢。然而,出色的科学家和普通的实验员之间的差别可能就在这个地方:洛伦茨觉得这不到千分之一的误差所带来的巨大影响从常理来说不可思议,此事必须有个数学解释。随后的几天里,他和两位程序员一起再次重复了两种不同初值的仿真,证实了他悟出的道理:由于该数学模型对初始条件具有高度敏感性,一个微小的初始误差随着反复迭代计算最终酿成巨大的结果差异,导致了模型未来行为的“不可预测性”!
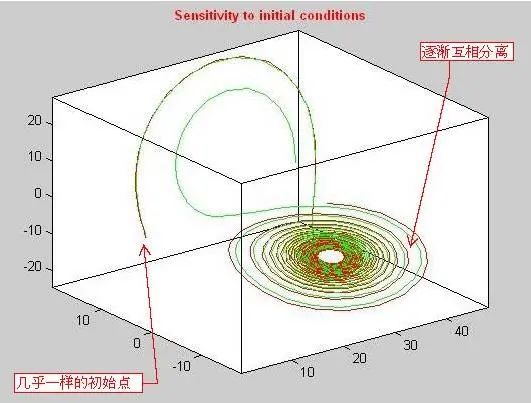
对初始条件的高度敏感性
洛伦茨把他的发现写成了论文“确定性的非周期流”,于1963年发表在《大气科学》杂志(“Deterministic nonperiodic flow”,Journal of the Atmospheric Sciences, 20: 130-141, 1963)。
洛伦茨当时觉得他发现的可能只是流体力学中湍流的一个新特征,投稿时把论文标题拟定为“确定性的湍流”。但杂志编辑对此颇有怀疑。于是他把“湍流”改成了“非周期流”。洛伦茨在论文中指出:“两个状态之间不被察觉的微小差别可能最后演化为巨大的不同……因此,如果在观察当前状态时不管有什么样的误差——在任何真实系统中这些误差是不可避免的——那么对于一个不太久远的未来瞬间状态做出任何可接受的预测都将是不可能的……非常长期的准确天气预报看来并不存在。”当年洛伦茨估算,准确的天气预报最多在两周时间之内可以做到。事实上,今天在高速计算机和大数据支持下,这个时间段也达不到三周。
在论文末尾,洛伦茨诚挚地感谢了巴里·萨尔茨曼和艾伦·费特。接下来,他在另一篇论文中也同样地致谢了玛格丽特·哈密顿。
在1963年这篇里程碑式的论文中,洛伦茨给出了刻画上述3个主要变量的非线性方程组,即今天著名的洛伦茨系统或洛伦茨方程:
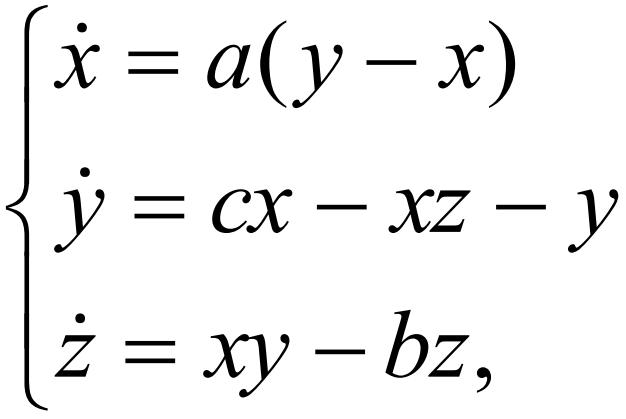
当参数 a = 10,b = 8/3,c = 28时,洛伦茨方程的解在三维空间中的轨道呈现一个漂亮的双涡卷形状的“吸引子”(attractor)。
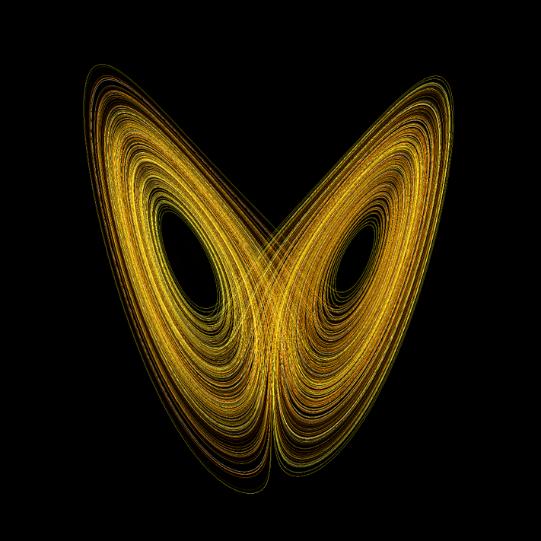
洛伦茨吸引子
这个后来被称为“洛伦茨吸引子”的几何对象是空间中一些带稳定性的点的集合,具有某种动力学的吸引性,故称为吸引子。但这个点集并不直观可见。计算机画出来的可视图只是绕着吸引子运动的方程的解轨道,它处于一种不寻常的永不发散、永不休止、并且是非严格周期的“混沌”(chaos)运动状态。其中,混沌轨道的不发散特征是由它的全局有界性决定的,而无休止的运动行为则把它区别于通常的骨牌效应。此外,解轨道的非严格周期性展现出它密集的近似周期性运动,但又不会严格地重复过去(用洛伦茨的原话来说,就是“solutions which never repeat their past history exactly”)。
此外,这个微分方程组的解由初始条件唯一决定,它是完全确定性的。从方程式可以看出,它没有诸如噪声或外来干扰的随机因素。但系统对初始状态值具有极高的敏感性,让它的解轨道在长时间之后的状态变得不可预测。人们把这种特性称为“确定性的随机”或“确定性的混沌”。由于混沌系统的解是确定性的,它可以用完全相同的初始条件来重演,但它又具有与不可复制的白噪声相同的各种随机特性,因此在工程应用中能派上一些特别用场。
对非专业人士来说,大抵上可以这样直观地去理解混沌系统及其混沌特性。

幕后英雄艾伦·费特和玛格丽特·哈密顿
[Artwork by Olena Shmahalo《Quanta》2019-5-20]
这里回顾一下历史是蛮有趣的。洛伦茨的上述论文并没有使用chaos一词。在科学文献中,chaos一词最早由MIT的数学家诺伯特·维纳(Norbert Weiner)1938年题为“The homogeneous chaos”的论文中开始使用,但那是完全不一样的数学概念。第一次正式用chaos来描述系统对初始条件极端敏感特性的,是已故数学家李天岩(1945-2020)和他的导师詹姆斯·约克(James A. Yorke,1941-)在1975 年发表的题为“Period three implies chaos”论文中的著名Li-Yorke定理。不过那是离散系统的混沌,是另一个论题了。
洛伦茨1963年这篇科学发现报告发表后,初时只有几个气象学家关注。美国科普畅销书作家詹姆斯·格雷克(James Gleick)1987出版的名著《混沌学传奇》(Chaos: Making a New Science)中说:“洛伦茨的这篇论文,在1960年代杂志上每年会被引用一次。可是二十年后,它每年被引用的次数超过一百。”今天,这篇文章已被引用两万六千多次。
顺便说说,洛伦茨系统属于所谓的耗散系统,其耗散量由流体粘度决定,缺失的能量则依靠热能补给。后来人们知道,许多别的耗散系统都可以产生混沌吸引子。此外,也有许多能量保守系统即哈密顿(Hamilton)系统也可以产生不同类型的混沌,但那又是另一个论题了。
开始时,洛伦茨把他的发现比喻为“海鸥飞翔引起了暴风雨”。后来,他接受了一位气象学家朋友Philip Merilees的建议,在1972年把他的一篇论文取题为:“在巴西的一只蝴蝶拍打一下翅膀会在得克萨斯州引发一场龙卷风吗?”于是,后来的科学文献、文学作品和人们日常生活里便有了一个新成语:“蝴蝶效应”(“butterfly effect”)。
洛伦茨吸引子酷似一只蝴蝶。扫码阅读“蝴蝶效应”集智百科词条
洛伦茨在他1993年出版的科普著作《混沌的本质》中还有另一种比喻:“一个人在中国打个喷嚏也可能会让纽约的人们去铲雪。”

UCL Press,USA,1993(中译本,1997)
显然,“混沌”的本质就是对初始条件的高度敏感性。可是,很多事物对初始条件具有高度敏感性的这种观察或认知,其实古来有之。
远至孔子(前551-前479)的《礼记·经解》,其中《易》里就说过:“君子慎始,差若毫厘,缪以千里。”古希腊哲学家亚里士多德(前384-前322)也说过:“对真实性极小的初始偏离,往后会被成千倍地放大。”近代物理学家詹姆斯·麦克斯韦(James Clerk Maxwell)在1873年亦说过:“系统初始状态的一个无穷小变化可能会引起该状态在有限时间内出现有限的偏差,这样的系统称为是不稳定的……并且会使得对将来事件的预测成为不可能。”数学家雅克·阿达马 (Jacques Hadamard) 在 1898 年也提到,“初始条件中的误差或者不精确性可能会使系统长时间的动力行为变得不可预测。”
到二十世纪初,通才数学家亨利・庞加莱 (Jules Henri Poincaré,1854-1912)在1908年他的书《科学与方法》中写道:“初始条件的微小误差在最后结果中产生极大差别的情况可能发生……于是预测变为不可能,从而我们就看到了许多偶然现象。”但是,所有先贤们的思想、观念和知识都停留在或者说局限于哲学和数学的思辨上,没有展示一个具体的科学实例。洛伦茨的伟大贡献,是他为这种极端敏感性和后来的混沌理论提供了一个简单又精准的物理系统的数学模型。不过,严格的混沌数学理论并不归功于洛伦茨。
现代混沌数学理论的鼻祖,是刚才提到的那位通才数学家庞加莱。1887年,瑞典国王奥斯卡二世(Oskar, II)悬赏,征求太阳系稳定性问题的解答,期望解决天体力学中的三体甚至N体问题。国王组织了三位当时最有权威的数学家担任评委:魏尔斯特拉斯(Karl Weierstrass)、米塔-列夫勒(Magnus Mittag-Leffler)和厄米特(Charles Hermite)。在那次高端科学论文竞赛中,庞加莱以他对三体问题的研究成果获得了大奖。
得奖论文按规定要在瑞典皇家科学院数学学报(Acta Mathematica)上发表。其时学报有一位负责论文校对的25岁年轻人Lars E. Phragmen,那时他是个数学爱好者,阅读庞加莱论文时发现有个地方老绕不过去,于是便去询问作者。庞加莱在试图作出解释的过程中发现原文有错,连他自己也绕不过去。
在这种时候,诚实的数学家可能会选择放弃,不诚实的数学家可能会含糊其辞敷衍了事。而这位顶尖的数学家庞加莱呢,在重要错误面前,深思熟虑之后彻底地改变了原来沿用的传统定量分析方法,以全新的定性分析方法重新探讨了这个数学上极其艰深的问题。此举让庞加莱开启了二十世纪动力系统定性理论、特别是混沌数学理论的先河,尽管该得奖论文拖延到1890年才问世(13卷,1-270页)。

Henri Poincaré Stephen Smale
因为说到混沌的数学理论了,还得先把它说得更清楚一些,才能回去把洛伦茨的故事讲完。
庞加莱对三体问题动力学作了精辟的定性分析之后,时间一下子过了半个多世纪。其间,除了大数学家乔治·伯克霍夫(George D. Birkhoff,1884-1944)和安德烈·柯尔莫哥洛夫(Andrey N. Kolmogorov,1903-1987)的贡献之外,还有非常重要但并不广为人知的玛丽·卡特赖特(D. Mary Cartwright,1900-1998)和约翰·李特尔伍德(John E. Littlewood,1885-1977),1945年间两人合作发展了无线电工程问题诱导出来的van der Pol振子的“奇异吸引子”(strange attractor)的数学理论。
十二年后,1957年斯蒂芬·斯梅尔(Stephen Smale,1930-)从密歇根大学数学博士毕业,在普林斯顿高等研究院(IAS)访问了一段时间之后,在国家自然科学基金资助下于1959年底来到了巴西里约热内卢著名的纯粹和应用数学研究院(IMPA)做博士后研究。这段时间他经常到沙滩去晒太阳,觉得沙滩的喧闹丝毫不会影响他深入思考各种数学问题。
年轻的斯梅尔在一篇自己感到自豪的文章中提及了他的一个“猜想”:“混沌不存在!”("chaos doesn't exist!")但是,他很快就接到 MIT 的数学家诺曼·莱文森(Norman Levinson,1912-1975)的来信,给他举了一个反例,同时向他介绍了卡特赖特-李特尔伍德的研究成果。后来,斯梅尔在1998年为《数学信使》(Mathematical Intelligencer)写的一篇题为“在里约热内卢海滩上发现马蹄”的文章中回忆道:“ [当时] 我夜以继日地工作,试图解决这个挑战……我最后说服了自己,莱文森是对的而我的猜想是错了。混沌已经隐含在卡特赖特-李特尔伍德的分析之中!现在迷团已经解开,是我作出了错误的猜测。但是在这个学习的过程中,我发现了马蹄!” ——好一个庞加莱式的数学家!
斯梅尔的“马蹄”理论可以用下面的示意图作一个简单解释。想象一个映射f把左上角的椭圆状面积投影到左下角的马蹄形面积去。它可以通过右面的压缩、拉伸和折叠三步操作而合成。然后,把马蹄放到左上角去取代椭圆的位置,再次用映射f投影到左下角去,这也可以通过同样的压缩、拉伸和折叠三步操作而完成。至此,做完了二次迭代,f2。然后,再重复同样的步骤,直到完成 n 次迭代,fn。理论上,n→∞,便可以得到密密麻麻无穷多个点,是前面所有大大小小马蹄的交点集合,称为康托(Cantor)集。容易看出,开始时在椭圆上相距很远的两个点,通过多次映射(反复压缩、拉伸和折叠)之后,会被转移到非常接近的相邻位置上。现在,如果从任意两个无论怎样接近的不同点出发,进行逆映射f-n,便会发现当n越来越大时,两条迭代轨道就会分离得越来越远,即开始时极小的差别会导致后来极大的差别。直观地说,fn把开始离得很远的两个点映射到康托集里非常接近的相邻位置上,而f-n则完成相反的工作。这个f称为斯梅尔马蹄映射。斯梅尔的马蹄理论用清晰具体的数学方式来表达并严格证明了混沌的最基本属性:对初始条件的极端敏感性。
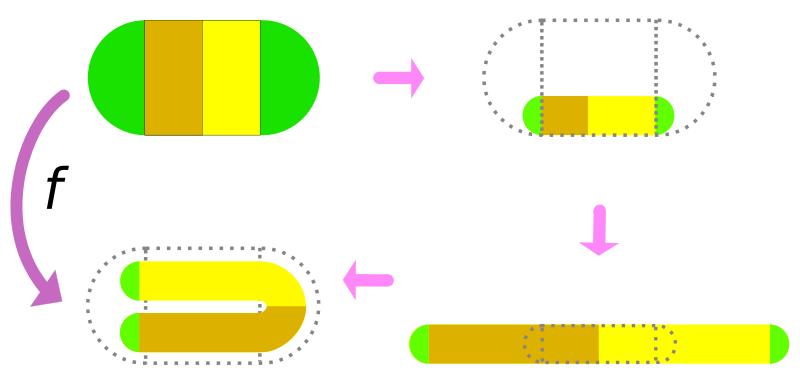
斯梅尔马蹄映射示意图
斯梅尔是非常有个性的数学家。1968年,约翰逊总统的科学顾问Donald Hornig 在《科学》(Science) 杂志刊文批评斯梅尔,说他领着国家自然科学基金去巴西沙滩晒太阳:“数学家们一本正经地提出要纳税人认同数学创造应该由公款资助到里约热内卢去躺沙滩……”多年以后,斯梅尔在上面提及的1998年文章“在里约热内卢海滩上发现马蹄”中对Donald Hornig作出了公开的反驳,说自己在里约热内卢沙滩上所作的数学创造“正是马蹄理论和高维 [所有高于4维] 庞加莱猜想的证明”,其中后面一项成就让斯梅尔荣膺1966年菲尔兹奖(Fields Medal)。

继续回顾历史,还有很多故事。前面说到,在数学文献中第一次正式用chaos来描述系统对初始条件极端敏感特性的,是1975年的李天岩-约克(Li-Yorke)定理。而最早把英文chaos翻译为中文“混沌”的,是北京大学荣休教授朱照宣先生(1930-)。这一名称引来许多有趣的中国神话故事。已故郝柏林院士(1934-2018)在他英文版《混沌》扉页以及《湍鉴—混沌理论与整体性科学导引》一书前言中,都引用过《庄子·应帝王》中的一句话:“南海之帝为倏,北海之帝为忽,中央之帝为浑沌”。其中,倏和忽后来变为成语“倏忽之间”,而古时的“浑沌”就是今天的“混沌”。中国道教始祖老子(前约571-前471)留下《太上老君八十一化图》,其中第二化曰:“……空洞之中,又生太无,太无之内生玄元始三气,三气相合,称为混沌”。就是说,古人心中的宇宙从无到有,由某种混沌状态开始。
即使以今天的科学观来看太阳系、银河系、以至整个宇宙,都可以把它们看作是混沌系统。首先,这些系统长期在如常运行,既不发散也不休止。其次,在天文时空尺度下,并没有严格周期运动的天体。要计算周期就得使用时间。我们今天使用的历法,俗称阳历,是天主教皇格里哥利13世(Gregorius XIII,1502-1585)在公元1582年设定的。在这个年历里,二月份只有28天,从而每年有365.2425天,但每四个世纪再加入一个闰年即增多1天的话历法会更准确,但这样一来平均每年就有了365.24242424天,因为这个做法让每年多出了26秒。不过,如果每隔128年再扣掉一个闰年,则每年有365.242190419天,400年将相差不到3个小时。目前没有比这个更精确的历法了。可是,它还不是数学意义下的严格周期。
国际度量衡总局(International Bureau of Weights and Measures)使用国际原子时间(International Atomic Time),规定每年的1月1日或7月1日对时间作出微调,每次增加或者减少原子钟定义的1秒。这样一来,尽管年有四季,冬去春来,人类实际上永远无法让“一年时间”严格周期化。因此,按前面对“混沌”的通俗理解,所有的天体在天文时空尺度下都是混沌系统——看来在宇宙完全坍塌之前大概就是这样。

现在再回来,继续说洛伦茨的故事。
许多科学家有一种共识,二十世纪科学史上三件最重大的事件是相对论、量子论和混沌论。相对论界定了牛顿力学有效的最大时空界限,就是当物体运动接近光速以及在十亿光年的大尺度宇宙空间里,牛顿力学不再适用;量子力学则界定了牛顿力学有效的最小时空界限,就是在微观世界里牛顿力学不再适用;而混沌论则打消了确定性意味着一切均可预测的信念。
在经典物理学中,著名数学家皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace,1749-1827)代表了他那个时代绝大部分人的科学观,认为如果一个确定性的系统有确定的初始状态,那么这个系统在未来所有时刻的状态都已经被完全确定了并且可以通过精确无误的计算而获得。他说:“我们可以认为宇宙的现在是由它的过去来决定的;现在也是决定未来的原因。如果有一位智者在某一时刻获知了自然界一切物体的位置和相互作用力,并且他具有超常的数据分析能力,那么他就可以把宇宙这个最庞大的物体直至到原子这个最细微的颗粒全都囊括到一个公式中去。对于这位智者来说,没有什么东西是不确定的——宇宙的未来会像它的过去一样完全呈现在他的眼前。”洛伦茨让拉普拉斯这段名言变成了“魔咒”(Demon)。
洛伦茨的非凡科学发现让他在1991年荣获被誉为“日本诺贝尔奖”的京都奖(Kyoto Prize),“奖励他发现了‘确定性混沌’这一杰出科学贡献,它是深刻地影响了广泛基础科学领域的一条原理,揭示了牛顿以来人类对自然认知的又一次翻天覆地的变化”。该奖励给洛伦茨颁发了一幅奖状、一个20K金奖章,以及5千万日元(折合人民币3百多万元)的奖金。历史上,第一次京都奖在1984年颁发,获奖者是洛伦茨在MIT的校友、数学家克劳德·香农(Claude E. Shannon),奖励他在信息论方面的奠基性贡献。

Kyoto Prize颁奖典礼
洛伦茨一生获得过不少荣誉和奖励。他于1969年获美国气象学会Carl-Gustaf Rossby研究奖,1973年获英国皇家气象学会Symons金质奖章,1975年当选为美国国家科学院院士,1981年当选为挪威科学与文学院外籍院士,1983获瑞典科学院Crafoord 奖,1984年获英国气象学院授予荣誉院士,1989年获美国富兰克福研究院颁发Elliott Cresson奖章。此后,洛伦茨于2000年获世界气象组织授予国际气象组织奖,2004年获俄罗斯国家科学院授予罗蒙洛索夫金质奖章,并获荷兰艺术与科学院于1888年设立、十年颁发一次的Buys Ballot奖章。洛伦茨生前最后一次演讲是2008年初在意大利罗马接受Tomassoni奖时的领奖演说,题目依然是“蝴蝶效应”(“The butterfly effect”)。
洛伦茨是个古典型科学家。他一生发表了61篇论文,任职后至离世平均每年发表1篇,其中58篇是他自己一个人写的,另外3篇分别和一位同事合作,但没有他的导师。记录表明,他33岁时发表第一篇论文,在50岁以前仅发表了18篇,而60岁以后却发表了31篇。他的发文高峰期在45-75岁之间。他人生最后一篇论文也是自己写的,去世后于2008年8月由Physica D杂志登出,题为“Compound windows of the Hénon map” (vol.237,pp.1689-1704)。
洛伦茨晚年还经常做学术演讲
洛伦茨为自然科学和社会科学创下了一个不朽的奇迹,然而他的生平却相对简单。洛伦茨于1917年5月23日出生在康涅狄格(Connecticut)州的West Hartford。他父亲Edward Henry Lorenz(1882-1956)是MIT机械工程毕业生,母亲Grace Peloubet Norton(1887-1943)从他年少开始一直鼓励和引导他和高手下棋并做博弈游戏,十分注重他的智力发展。他的外祖父Lewis M. Norton是MIT教授,也是开设化工课程第一人。洛伦茨1938年从Dartmouth College获得数学学士学位,1940年从哈佛大学获得数学硕士学位,1941年独自在美国科学院院刊(PNAS)发表了第一篇论文“A generalization of the Dirac equations”。他接下来到了部队服役,二战期间在空军气象站当天气预报员。期间,1943年他在MIT完成了气象硕士学位,战后1948年在MIT取得了气象博士学位。他的博士导师James Murdoch Austin(1915-2000)是新西兰人,美国科学与艺术科学院院士,曾获得过总统颁发的自由勋章。洛伦茨的博士论文题为“应用水力学和热力学方程研究大气模型的新方法”。他毕业后留校在气象系任教,1962年晋升为正教授,1977-1981年间任系主任,1987年荣休,2008年4月16日因患癌症在家中离世,享年91岁。他夫人Jane Loban于2001年去世。他们有三个孩子:女儿Nancy和Cheryl、儿子Edward。
洛伦茨是个温文尔雅的谦谦君子。朋友们都说他“Modest and soft-spoken”。他喜欢野外跋涉和高山滑雪,还常常在学术会议之后去附近的山林远足。他去世时,女儿Cheryl对亲友说:“他两周半前还去爬山,一周前还和同事一起完成了一篇论文。”

洛伦茨 @ Mt Battie(Lorenz Center)
2011年,MIT成立了洛伦茨学术研究中心,秉承洛伦茨的旨意,“追求对气象学基本原理的认知”。研究中心的筹建者曾引述洛伦茨在2005年写下的一段话:“人们经常都会看到,纯粹理论研究的一点点成果,也许在很长时间之后,会导致连做该纯理论研究的科学家都始料不及的实际应用。”


21世纪是复杂性的世纪,理解混沌是探索复杂性的关键环节。在科学、工程中,混沌与非线性方法已经成为研究动态系统的主要手段,加深了对气候、生态、大脑、流行病等诸多复杂系统问题的理解,并在湍流、加密、数据分析以及生命科学中有广泛应用。在社会、商业领域,混沌理论在通讯、交通、金融市场、疾病与信息传播等问题中亦有诸多启发和应用。随着混沌现象的进一步系统研究和广泛应用,它正在从一套理论发展为一门科学。
原标题:《蝴蝶效应和混沌故事 | 陈关荣》

