圆周率日：π值3.1415926.......是怎么计算出来的
今天
是数学爱好者们
背诵圆周率
畅谈数学
和吃馅饼的日子~
2011年，国际数学协会宣布将每年的3月14日设为国际数学节。2019年11月26日，联合国教科文组织在第四十届大会批准宣布，3月14日为“国际数学日”。这个日子也是“国际圆周率日”。尽管除读音相同以外，π与Pie(派，一种食物)并无联系，人们还是乐于在圆周率日这一天烹制一块派，在上面摆上π的标志。
圆周率是圆的周长与直径的比值，一般用希腊字母π表示，是一个在数学及物理学中普遍存在的常数，也是最著名的无理数。
而将π与其他无理数区别开来的，正是它与圆的关系。π等于圆形之面积与半径平方之比，是精确计算圆周长、圆面积、球体积等几何形状的关键值。在分析学里，π可以严格地定义为满足sin x = 0的最小正实数x。
古往今来，数学家们乐此不疲地追求圆周率的精确数值，使得π成为迄今为止数学史上研究最多的数字。它究竟拥有怎样的魅力？
π是一个随机数生成器，我们永远无法知道它的精确数值。而计算的精确性，一度被作为衡量一个国家数学发展程度的标准。计算万亿位数的圆周率需要一个强大的计算机，因此，计算π值可被视作计算机的“压力测试”。如今，科学家通过超级计算机，已经将圆周率的数值精确到了小数点后62.8万亿位。
数学家们对代数的采用，激发了一种全新的看待世界的方式。计算π的下一个重大飞跃是微积分的发明，从那以后，数学家们开始研究无穷级数。
当我们将数学应用到现实世界，还会发现π在宇宙中无处不在，在我们的生活中无处不在。它实际上已经融入了宇宙、行星轨道、电磁波、河流、极光颜色、DNA结构、吉萨大金字塔……
数学家如何计算圆周率？
历史上的数学家们又是如何计算圆周率的呢？
一个由直线拼成的几何图形，可以由多个三角形以及矩形组成，计算周长、面积都相对方便，甚至可以用尺子丈量。但是对于一个圆而言，图形上的任何一处都是带有弧度的曲线，又该从何下手呢？
早在远古时期，伟大的劳动人民就发现圆的周长与直径之间有着不为人知的秘密。出土文物显示，古巴比伦时期的几何学家已经将圆周率推算到25/8（3.125）。
阿基米德
而最早的有记录的严谨算法可以追溯到公元前250年，古希腊著名数学家、物理学家阿基米德通过正多边形法计算圆周率。他作圆的内接和外切正6边形，然后倍增到正12边形、正24边形、正48边形，正96边形，最后手动得出π的下界与上界分别为223/71与22/7（即3.140845＜π＜3.142857)。
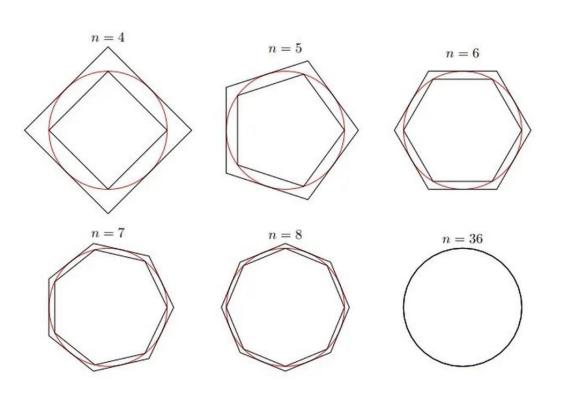阿基米德求圆周率的思路是首先构造圆内接多边形和对应的外切多边形。当边数足够大时，两个多边形的周长便趋近于圆周长的下界与上界
在中国，圆周率的记载可追溯到古算书《周髀算经》，其上记载 “径一而周三”，意思是直径为1的圆，它的周长为3，即取π=3。显然，该数值还不够精确。
此后，数学家先后借助割圆术、无穷级数等方法计算π的值。
公元263年，三国时期的数学家刘徽创立了割圆术，用以计算圆周率。他先从圆内接正6边形，逐次分割一直算到圆内接正192边形。他曾说，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”这段话包含了求极限的思想，为我国古代的圆周率计算确立了理论基础。
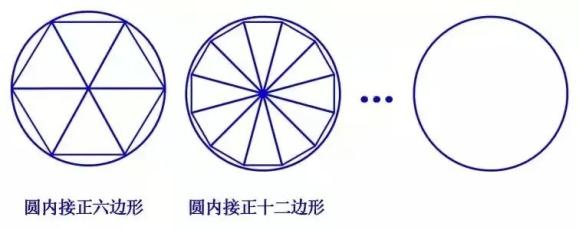割圆术：用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率
刘徽在得出圆周率=3.14之后，发现数值还是偏小，于是继续割圆到1536边形，求出3072边形的面积，终于得到令自己满意的π值3.1416。
公元480年左右，南北朝时期的数学家祖冲之不满足于前人的成就，决定攀登新的高峰。他通过割圆术长期刻苦钻研，在儿子祖暅的协助下，反复测算，终于求得了精确度更高的圆周率。《隋书•律历志》中记载了他的成就：
“宋末，南徐州从事史祖冲之更开密法，以圆径一亿为一丈，圆周盈数3丈1尺4寸1分5厘9毫2秒7忽(3.1415927丈)，朒数3丈1尺4寸1分5厘9毫2秒6忽(3.1515926丈)，正数在盈肭之间。密率：圆径113，圆周355。约率：圆径7，周23。”
祖冲之
从上述文字记载来看，祖冲之对圆周率贡献有三点：
（1）计算出圆周率在3.1415926到3.1415927之间，在世界数学史上第一次把圆周率精确推算到小数点后7位。直到15世纪，阿拉伯数学家阿尔•卡西计算到小数点后16位，才打破祖冲之的纪录。
（2）祖冲之明确地指出了圆周率的上限和下限，用两个高准确度的固定数作界限，精确地说明了圆周率的大小范围，实际上已确定了误差范围，这是前所未有的。
（3）祖冲之提出约率20/7和密率355/113。这一密率值在世界上属首次提出，所以有人主张叫它“祖率”。在欧洲，德国人奥托和荷兰人安托尼兹得到这一结果，已是16世纪。祖冲之是怎样得出这一结果的呢？他应该是从圆内接正6边形、12边形、24边形……一直计算到12288边形和24576边形，依次求出它们的边长和面积。
后来，随着处境和时代的变化，祖冲之的研究兴趣转变到了机械制造方面。其中最突出的成就是重造了指南车、制造了水碓磨。
尤其值得一提的是，祖冲之研究球体积的算法，可惜没有完成，这个未竟的事业被祖暅彻底解决了。他还总结出了一条公理，即：“幂势既同，则积不容异。”意思是说，位于两平行平面之间的两个立体，被任意一个平行于这两平面的平面所截，如果两个截面的面积恒相等，则这两个立体的体积相等。这就是著名的“祖暅公理”。这一公理一直到17世纪才被意大利数学家卡瓦列利发现，比祖暅晚了一千多年。
祖冲之去世距今已有一千五百余年，但他锲而不舍、钻研继承的求知精神，求真求实、理性批判的怀疑精神，开拓变革、超越前人的创新精神，不畏权势、敢于坚持真理的勇气成为后人特别是后世科学家的榜样。
数学家对精确π值的追求
不曾停歇
如同寻根究底的科学精神
没有止境
回顾完圆周率的发展史
让我们向千千万万的数学家们
致以崇高的敬意！
综编：科普中国、科学大院微信公众号
算法与数学之美微信公众号（作者：数学吧主）
《月读》2017年第9期
原标题：《圆周率日：π值3.1415926.......是怎么计算出来的》