原创 金诚 央视网 收录于话题#煮酒18个
1993年6月23日,剑桥大学牛顿研究所演讲厅里,进行着20世纪最重要的一次数学讲座,题为《模形式、椭圆曲线和伽罗瓦表示》。
光看这题目,先吓退许多人,连现场的200名数学家也只有1/4能听懂。但当时真实的场面却是如此火爆,学者、记者挤满了演讲厅,迟到的人只能站在走廊,踮起脚透过窗户看。
他们等待的不是黑板上那些奇形怪状、秘密麻麻的希腊字母和函数,而是一个历史性时刻:困惑人类358年的“费马大定理”将被最终攻克。
证明人最后一次转向黑板,手拿粉笔,充满仪式感地写下最后几行论证公式后,缓缓转向台下听众,说道:
“我想我就在这里结束。”

证明人在板书后,来源:纪录片《费马大定理》
“咔擦”,一道闪光灯亮起,打破了沉默,继而响起雷鸣般的掌声,经久不息。消息立刻传遍世界,这是当时绝对的热搜。《世界报》的头版称“费马大定理获得解决”,《纽约时报》头版写道《终于欢呼“我发现了!”久远的数学之谜获解》,《人物》杂志将他与戴安娜王妃等人列为“年度25位最具魅力者”之一。
这位证明人就是旅美英国数学家安德鲁·怀尔斯。
然而他的这次证明,竟然错了。

怀尔斯照片,来源:视觉中国
世纪玩笑
安德鲁·怀尔斯自小迷恋解数学题,1963年的一天,10岁的他在泡图书馆时,手头拿着一本叫《大问题》的书,当他翻到“费马大定理”那一页,被一个简洁明快的数学公式深深吸引住。
“为什么如此简单的公式,300多年来所有的数学大师都无法解决?”一颗好奇的种子埋进了小怀尔斯的心里。
故事要从费马本人讲起。
费马出生在17世纪的法国,本职是一名公务员。闲暇时间也爱做数学题,这一做可不得了,他顺带创立了概率论、发现了解析几何原理,启发牛顿创立了微积分,被称为“业余数学家之王”。
他还有另一大兴趣:数论,玩的是纯数字游戏。“数学王子”高斯说过,“数学是科学的皇后,数论是数学的皇后”。可见是多么高智商的领域。
一天,费马翻阅《算术》,继续做题,突然被毕达哥拉斯定理(勾股定理)——a2+b2=c2的公式之美,激发了灵感,他想:以此类推,有没有可能找到X3+Y3=Z3的整数解?有没有可能找到X4+Y4=Z4 的整数解?……
进一步,他断言当整数n >2时,Xn+Yn=Zn没有正整数解。
这就是“费马猜想”。至于证明,费马发挥了一贯作风,只给结论、不加证明。他在书边空白处写道:“我有一个对这个命题非常美妙的证明,但这里空白太小,写不下啦。”
这一玩笑事小,却引发了数学家们长达360年的抓狂和艰辛探索。
例如,18世纪的数学之神欧拉,创造性地引入“虚数”,证明在 n=3 的情况下,费马猜想是成立的,然后就啃不动了。后来,高斯、柯西等伟大的数学家也没有解开过。失败的大数学家越多,费马猜想的神秘味道就越浓。
20世纪后半叶,计算机的发明让很多数学问题可以用“暴力计算”解决。计算机解决了当n小于25000的时候,费马猜想都是成立的。但从逻辑上讲,n具体数值再大,也不能保证在n+1时成立,必须进行严格的数理证明,形成逻辑闭环。
自从图书馆的那过目不忘的一眼,小怀尔斯与费马大定理结上了缘分,“从第一天起,我知道我永远不会放弃它,我必须解决它。”
“躲进小楼成一统”
1975年,怀尔斯成为了剑桥大学博士。在选择方向时,由于费马猜想耗时耗力,也没啥应用价值,导师建议他攻读“椭圆曲线”。权衡之下,怀尔斯暂且放下对定理的证明。
可没想到,正是这“椭圆曲线”歪打正着。怀尔斯与费马大定理缘分未尽。
时间在平淡中到了1984年秋。有一天,他去德国黑森林州参加学术会议,听到了数学家弗赖讲,椭圆曲线领域的“谷山-志村猜想”,是证明费马猜想的关键核心步骤,只要证明这一猜想,费马猜想就会迎刃而解。
怀尔斯内心受到了极大震动,大腿一拍:证明费马是梦想,椭圆曲线是专长,真是踏破铁鞋无觅处啊!他决定攻克“谷山-志村猜想”。
这个“谷山-志村猜想”,相当于“数学之桥”。在数学的汪洋大海中,数论啊、概率论啊、几何啊等等,好比大海中的孤岛,彼此隔离,缺乏联系。证明了谷山-志村猜想,就等于搭起了一座桥梁,让跨界知识融合互鉴,推动数学问题在更高层级解决,解决单一知识无法破解的局限。
不过,谷山-志村猜想也是难度极高,提出30年来,还无人破解。
对此,怀尔斯做了一生中最重要的决定:放弃所有与费马大定理无关的学术报告,准备十年面壁。
第一步,“独上高楼”。
怀尔斯钻进了自家的楼阁,深入到数学大厦中最幽暗深邃的角落,这一钻就是7年。除了自己的新婚妻子知道他在干什么,他对外人闭口不提。为了掩人耳目,他每隔6个月左右发表一篇小论文,让同行觉得他在干活,但不知道是攻克费马大定理。

怀尔斯在阁楼中演算,来源:纪录片《费马大定理》
这样做的风险是极高的。一般来说,学术之间加强交流,在互鉴中纠正错误,才能防止钻进死胡同。怀尔斯是孤注一掷,即使哪里错了,也没人提醒。
第二招,“旁征博引”。
怀尔斯发现攻克费马猜想的全部数学技术,已经被反复用了100多年,从“无穷递降法”“归纳法”到“反证法”,从伽罗瓦群、模方法、岩沢理论,到科利瓦金弗莱切方法,既有古代的也有现代的。
几年中,他将所有公开发表的相关文献中的方法和技术都尝试过后,绝望地写道“很可能解决这个问题的方法是现代数学无法实现的,或许所需要的方法再过100年也不会被发现。因此,即使我的思路是正确的,我却生活在一个错误的世纪中。”
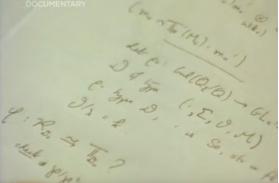
怀尔斯的证明过程片段,来源:纪录片《费马大定理》
第三招,“外部力量”。
后期,怀尔斯借助给系里研究生授课的机会,将证明中几千个逻辑链条需要核对的部分,一点一点地拿给学生们课堂讨论,提出反驳。这既有助于检验自己的工作,也能很好地在授课中把秘密伪装起来,不会引起同行的任何怀疑。
就这么7年过去了,怀尔斯终于完成了“谷山-志村猜想”的证明,他也顺理成章证明了费马大定理,是时候向全世界公布了。
绝境中的“决斗”
怀尔斯在进行完文章开头那次世纪讲座后,还将接受极其严格周密的审查,他将手稿递交给《数学发明》杂志。主审格外重视,不像通常只指定两个或三个审稿人,而是六个审稿人,200页的特大型的论证被划分为6章,每一位审稿人专门负责其中一章。
两个月后,一盆冷水浇在了怀尔斯头上。在“科利瓦金弗莱切方法”有关论证的关键环节有一个错误!数学证明就是这样,几千个逻辑链中即使有一环没衔接好,那整个证明将毁于一旦。
毕竟,曾经有无数大师倒在了费马大定理面前,数学界对这样的结果并不惊讶。他们一边安慰怀尔斯,声称主体部分已经是了不起的成就了,一边希望怀尔斯公开手稿,让数论研究者共同来解决。
怀尔斯拒绝了。因为他不想为别人做嫁衣,他执拗地重新回到阁楼去了。
半年过去了,寒冬已经来临,证明依然毫无突破。怀尔斯在绝境之下找来审稿人之一、也是自己的学生泰勒,一起来攻关。
又过了半年,不仅没有进展,而且泰勒跟着怀尔斯一齐,陷入了数学的迷宫。
转眼新一年的夏天来了,怀尔斯是“为伊消得人憔悴”,在沮丧中准备承认失败。泰勒却鼓励老师“再坚持一个月吧,如果到9月底还没有突破的迹象,我们就放弃。”
无论成败与否,作为数学家的怀尔斯只想知道到底错在了哪里,死也要死个明白。他决定最后一试。
9月19日,星期一早晨,怀尔斯在桌子旁,检查着那个错误一环。蓦然回首,仿佛有个“苹果”砸到了他头上:单靠岩沢理论不足以解决,单靠科利瓦金弗莱切方法也不足以解决,但两个方法互补在一起,不就巧妙破解了吗?
怀尔斯激动得热泪盈眶,足足呆滞了20多分钟。这是8年苦心演绎,14个月逼向悬崖的智力决斗啊!
1994年10月25日11点4分11秒,怀尔斯点击电子邮件,发送出两份手稿——《模椭圆曲线和费马大定理》和《某些赫克代数的环论性质》。
至此,费马大定理得以完全证明。

1997年,怀尔斯获得沃尔夫斯科尔(Wolfskehl)奖,来源:视觉中国
“我们必须知道,我们必将知道”
不禁要问,耗费一生证明这个古老的数学难题有什么意义呢?
历史总是有一些无用之用。整个费马大定理的证明过程,引致了很多数学研究的应用,例如今天区块链技术中的椭圆加密,再例如比特币。
回顾怀尔斯的成就,我们看到了一个数学家在追求真理、荣誉和智力高峰的过程中,是如此地执拗和孤僻,甚至不愿意分享与合群。其实,达尔文、牛顿等顶尖天才,都有过为争取独享的荣誉而想尽“花招”。这何尝不是推动人类进步的动力呢?
不过,怀尔斯最终的成功,还是离不开“出圈”的能力,他借助了许多跨界的数理技术,借助了外脑的智力,这才得以飞到高空,俯瞰此山中。
还有一个疑点,综观怀尔斯的论证,发展了一系列数学技巧,如谷山-志村猜想、伽罗瓦群、科利瓦金弗莱切方法等,这些都不是费马时代所知道的知识。如果费马不是用怀尔斯的方法,他又是用什么进行了那个“美妙证明”的呢?
答案就用伟大数学家希尔伯特墓志铭上的话来总结吧——“我们必须知道,我们必将知道”。
参考文献:
《费马大定理:一个困惑了世间智者358年的谜》,[美]西蒙·辛格
纪录片《费马大定理》,BBC
▼
更多新闻,扫描二维码
关注央视网
©央视网
将央视网设为星标
好新闻不错过
原标题:《这篇文章你可能看不懂》
