原创 Helen 罗博深数学

文 2459字 阅读时间 5分钟

导语

人教版的教材惊现“利用相对论证明了勾股定理”大乌龙，网友：你数学是体育老师教的吧！

勾股定理，相信大家都很熟悉了，直角三角形两条直角边的平方和等于斜边的平方，a⊃2;+ b⊃2; = c⊃2; 都要背烂了。可就在最近，人教版的教材中的“爱因斯坦对勾股定理的证明”惊现大乌龙——“利用相对论证明了勾股定理”。

我们给大家还原一下大型翻车现场。

首先，E=mc⊃2;这里的c是指光速，和斜边没有任何关系。

其次，这里的E是指物体固有的质能。不同物体的质量m是不一样的，像这里的小三角和大三角，显然不能用同一个m来表示。

地铁大爷脸逐渐僵硬。关于相对论的知识，我们稍后再进行讨论。

作为典型的别人家的小孩，我们还在玩泥巴的年纪，爱因斯坦就证明了勾股定理。虽然爱因斯坦当时并没有把整个证明记录下来，但是他的助手和其他物理学家依然尽量还原了他的巧妙证明。

第一步，我们加一条辅助线，是斜边上的高。注意这条高和斜边 c 是垂直的。

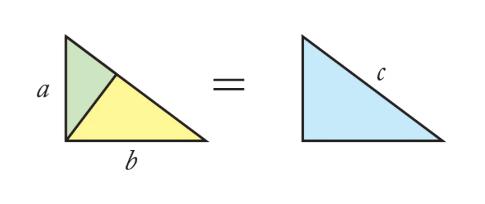
根据我们学过的判定方法寻找“角角角”。首先它们都是直角三角形，90度是第一个角。第二，绿和黄两个三角形分别和蓝三角形共用一个角。因为三角形的内角和都是180度，剩下的那一个角一定也相等。所以根据角角角的判别方式，他们一定相似。

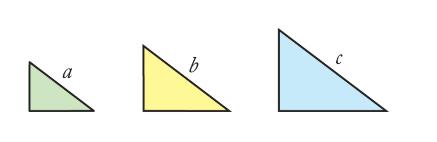
在这里我们用f来表示这个比例，那么绿三角形的面积就是fa⊃2;, 黄三角形的面积就是fb⊃2;，蓝三角形的面积是fc⊃2;。

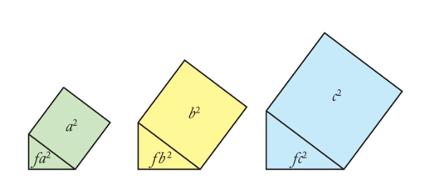
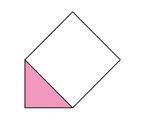
这个证明可比我们平时推导的要简单优雅得多。但是一时半会儿可能还是有些让人难以理解，尤其是最后一步。为什么同样形状的三角形，占边长为斜边的正方形的比例是相等的？我们不妨从一个最特殊的例子来观察一下。想象一个等腰直角三角形，我们取斜边上的正方形，就像折叠信封的形状一样，

我们知道每个等腰直角三角形的面积都是相应斜边上正方形的1/4，与三角形的大小没有关系。

说完了勾股定理的部分，我们回到爱因斯坦和他的相对论。E = mc⊃2; 这个公式可谓是无人不知，无人不晓。我们今天就简单来介绍一下相对论。

相对论中的最重要概念就是参考系。有一句物理学的名言，大家可能都听说过，“这个世界上没有绝对的静止”。你静静坐在尘世喧嚣中，修篱种菊。那是你相对于地球而言是静止的，地球是我们描述运动的参考系。毛主席的“坐地日行八万里，巡天遥看一千河”也说明了这个道理。尽管我们相对于地球可能是静止的，我们仍然随着地球的自转在运动。所以不标明参考系的运动都是在耍流氓。

在牛顿的经典力学中，相对于参考系静止的物体是不具有能量的。但是在相对论中，爱因斯坦认为相对于参考系静止的物体仍然是有能量的。这个能量可以与质量等价，这就是我们著名的质能方程，表示相对于参考系静止的物体的能量。这里的c是光速，是一个常数。和勾股定理里的斜边没有任何关系。

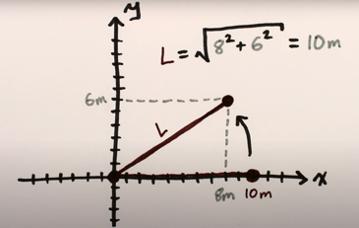
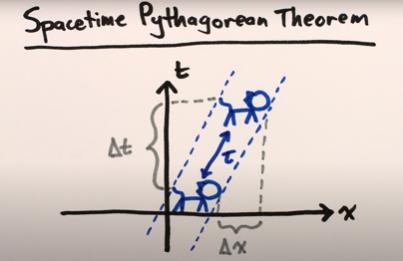
在狭义相对论里，我们常常用时空图来表示任意物体的运动。因为当一个物体的速度足够快，在它的参考系里，时间会膨胀（time dilation），长度会收缩（length contraction）。所以我们需要在时空图里，将时间和空间的变化都体现出来。

换句话说，坐在两艘速度不同的飞船里，两个宇航员对时间的感受不同，对空间的感受也不同，我们只知道光速是绝对的，那么我们怎么将不同参考系的时空“统一”起来呢？这就要用到勾股定理啦。

爱因斯坦和勾股定理固然有许许多多的羁绊，但是从来没有用相对论证明过勾股定理。这场大乌龙也教会我们，做学问是为了知识本身能带给我们的乐趣。所谓知之为知之，不知为不知，是知也。

下面这个这个视频，是开源学习社区expii的对勾股定理的趣味解说��！罗教授的Daily Challenge系列数学课程从Module0开始也有涵盖对勾股定理相关知识的系统讲解。其实不止是勾股定理和相对论，宇宙中的知识纷繁复杂，各种“权威”教材的解释众说纷纭。让孩子从小树立对知识的正确认识，培养发现错误的批判性思维，才是可以让他们可以受益一辈子的事。

· 感谢您的阅读 ·

原标题：《人教版数学教材：爱因斯坦和他的勾股定理？？？》