原创 Helen 罗博深数学

作者 | Helen

文 2013字 阅读时间约 7分钟

导语

本文作者Helen是CMU数学系大三学生、罗教授的忠实小迷妹。在一节罗教授的离散数学课堂上，“看着罗教授提笔画的那个奇奇怪怪的方阵”，她的思绪在这个方阵里弯弯绕绕，于是这里开始了一个下午的胡思乱想......

很久很久以前，有这样一个世界，这个世界由许许多多的迷宫构成，每个人都想要走到彼岸去。最简单的迷宫可能是这样的一个小方块，总共就只有两条路，怎么走都走得通。左边一条路，右边一条路，条条大路通罗马。

再复杂一点的迷宫，是一个小方阵。我们稍加思索，也能找到有几条通往彼岸的路，就像下图从小A通往小B的迷宫。

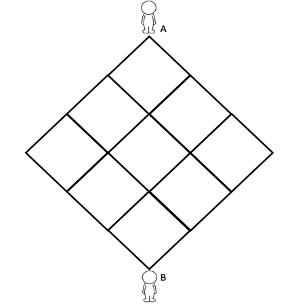
首先我们看看，小A要走到小B处，不管怎么走，我们都得往左下走三步，往右下走三步。如果想象不够直观，那我们挑两条路来走走看。是不是稍微有一点点感觉了？把蓝色歪歪曲曲的线段落整齐，其实得到的就是橙色线路的轮廓。

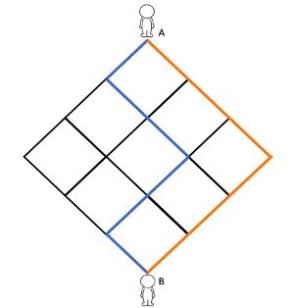
来表示，用来解决一些很实际的问题，比如，要我从五条不同的路里面选出任意三条，就表示一共有

种不同的选法。

想想看这和我们的问题有什么关系？

小A是个很执着的人，这个世界奇形怪状的迷宫和对岸的小B对他来说真的太可爱了。他看着窗外熙熙攘攘的行人，恨不得马上到达小B的那一边。通往小B的路究竟有多少条？要怎么走才不会迷路？于是他靠着窗户想了又想，就着布满雾气的窗户，一笔一画写出来这么几个透明的字：

右右右左左左

左右右左左右

小A的脑海里，沿着这两行指示，走出来两条路，一条蓝色的，一条橙色的。他想了想，一共要走六步，三步往左，三步往右，只要左左右右排列组合的顺序不一样，我们就能找到不同的路。那这样的话，每六步里面，我们选出三步往右走，剩下的三步自然就是往左走，也就等于选出了一条路。那么，我们知道一共有

条路通往小B 了！其实不光是正方形的迷宫。任何长方形的迷宫都可以这样解决。你能想到吗？

黑板上，罗教授改了几笔，擦掉了几条线，问题一下子变得复杂起来了。

我眼前又浮现出抱着膝盖的一个小A，跟罗教授的粉笔一起，回到了起点。小A知道自己心里缺了点什么的，这个迷宫里缺了一条路。每次小B 早上起来提着水壶给花浇水的时候，都看得到小A 在窗台上写写画画。小B 觉得他很可爱，于是也认认真真地看起了通向小A 奇形怪状的迷宫。

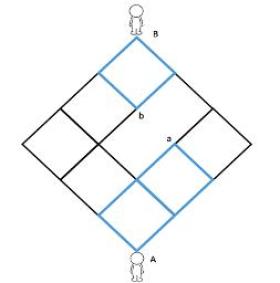
条路，a->A有

条路。我们每次在B->b 选一条，a->A 选一条，那么经过ba的路线一共有 2 x 3 = 6 种不同的路。也就是说，通往小A的路，只有

条。

罗教授看我们思考地很快，大笔一挥，又刷刷刷去掉了一些线路。

兜兜转转地，这两个小傻瓜怎么走也走不到一起。小A的心里一天比一天更荒凉下去了，他们之间的迷宫越来越奇怪了。再按照原来的思路，要涉及到好多不同的点和线，实在太复杂了。

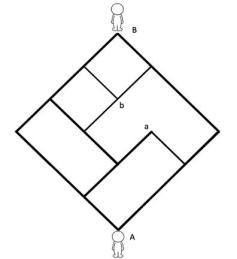
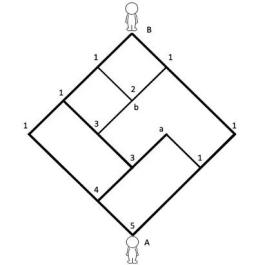
还记得小时候看一个笑话，说数学啊，你赶紧长大吧，该学会自己解决自己的问题了。可是二维空间里的小傻瓜啊，他们怎么解决自己的问题呢？是我们在解决这些乱七八糟的问题之后，悄悄地长大了吧。从此以后在各种各样的迷宫里跌跌撞撞，但愿还能像走今天的迷宫一样，化繁为简，找到方向。或许你的迷宫曲曲张张不知道有多少弯绕，或许这个世界迂回蜿蜒不知道有多少沟壑，但愿我们都再也不会迷路了。

* 本文内容属罗博深数学及其母公司Expii, Inc所有，如需转载请联系罗博深数学团队，未经授权请勿转载。欢迎转发本文与全世界的朋友分享数学、教育的乐趣。

往期精选

» 6年级儿子和伯克利大学生连打两天比赛：战胜自己，孩子就成功了一半

» 那些在网上传疯了的数学题（一）——几何篇

» 那些在网上传疯了的数学题（二）——代数篇

» 中学生也能看得懂的无穷问题！

» 孩子注意力不集中怎么办？

- 点击海报了解课程详情 -

150分钟免费体验课程火热放送中

原标题：《离散数学的转角遇到爱：向左走，向右走》