可快速关注我们
一、地图投影的概念
地球到底是什么样的?公元前6世纪,古希腊数学家毕达哥拉斯率先提出了“地圆说”。他在观察月食时,发现大地在月球上的投影是圆的,所以认为大地是完整的圆球体。他首次提出了“地球”这一概念。然而当时的人只能依靠推理和想象,没有机会见到地球的真面目。现在大家想要亲眼见一见地球,除了把玩地球仪,也可以摊开世界地图,遍览七洲四洋。不过世界地图真的只有平常见到的那一种模样么?“远看成岭侧成峰”,通过不同的角度去观察地球,她的风景自然也是不同的。如图1-1所示,这两幅地图与我们平日里所见的世界地图非常不同。
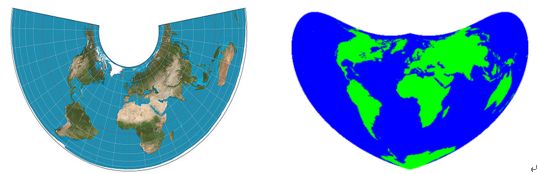
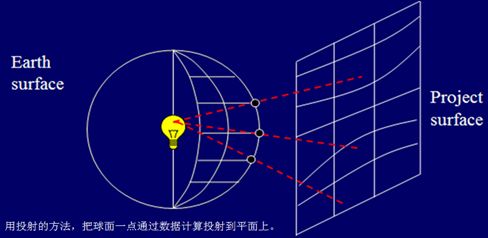
为什么同一个地球却能有这么多不同的地图表达呢?众所周知,地球是一个三维的椭球体,并且地球表面是不可展开面,而地图是一个二维平面。将三维的地球表面映射到二维平面的过程就是地图的投影。在投影过程中我们希望地图可以保持形状,距离和面积关系与地球表面完全相同。不幸的是,可以证明没有并且永远不会有这样一个完美的投影:由于空间维度的降低,每一种投影都必然会扭曲至少部分映射区域,如图1-2所示。因此,为不同的地图应用来设计和选择最合适的地图投影是一门权衡的艺术和科学。

除非压缩,拉伸或撕裂,否则它不能完全展平。
二、地理坐标系与投影坐标系
由于地图投影是按照一定的数学法则将三维地球表面投影转换到二维平面地图上去。因此我们需要在三维地球和二维地图上各自建立坐标系去定量描述每一个点的坐标,即建立起地面某点的地理坐标
与投影后的笛卡尔平面直角坐标
的函数关系,如图2-1所示。投影的一般公式为:
从公式中可以看出,计算平面直角坐标需要明确两个方面:地理坐标
和投影函数F。地理坐标
由大地测量坐标系决定,对于同一地理位置,在不同的地理坐标系中它的经纬度坐标也是不同的,而函数关系由地图投影方式决定,一般是选择最贴合某一区域、扭曲变形最小的地图投影。
1
地理坐标系的定义
地理坐标系 (Geographic coordinate system, GCS) 使用三维球面来定义地球上的位置。地理坐标系常常被误称为基准面,而基准面仅是地理坐标系的一部分。地理坐标系包括角度测量单位、本初子午线和基准面(基于旋转椭球体)。
(1)角度测量单位
角度测量单位通常使用度或者百分度,如图2-2左图所示,每一个点的坐标值由其经度和纬度值确定。图2-2右图将地球显示为具有经度和纬度值的地球,红色的水平线(或东西线)是等纬度线或纬线,蓝色的垂直线(或南北线)是等经度线或经线。这些线包络着地球,构成了一个称为经纬网的格网化网络。
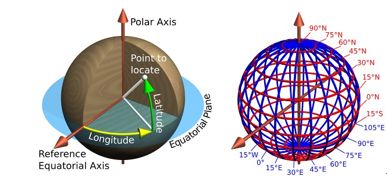
(2)本初子午线
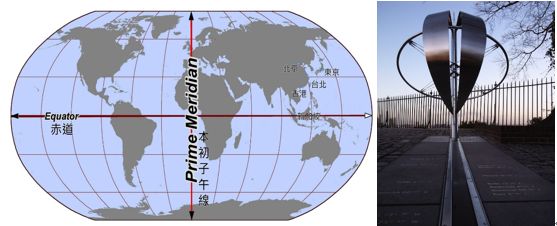
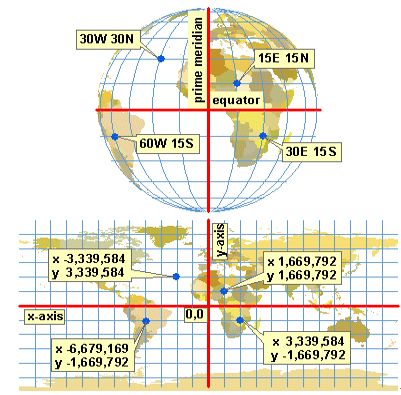
本初子午线又称为零经度线,对于绝大多数地理坐标系,本初子午线是指通过英国格林尼治的经线,如图2-3所示。其他国家/地区使用通过伯尔尼、波哥大和巴黎的经线作为本初子午线。位于两极点中间的纬线称为赤道。经纬网的原点 (0,0) 定义在赤道和本初子午线的交点处。这样,地球就被分为了四个地理象限,它们均基于与原点所成的罗盘方位角。赤道的下方和上方分别为南半球和北半球,而本初子午线的左侧和右侧分别为西半球和东半球。
通常,经度和纬度值以十进制度为单位或以度、分和秒 (DMS) 为单位进行测量。纬度值相对于赤道进行测量,其范围是 -90°(南极点)到 +90°(北极点)。经度值相对于本初子午线进行测量。其范围是 -180°(向西行进时)到 180°(向东行进时)。如果本初子午线是格林尼治子午线,则对于位于赤道北部和格林尼治东部的中国,其经度和纬度都为正值。
(3)大地水准面、参考椭球体、大地基准面的三级逼近
到目前为止,我们认为地球是一个完美的球体,但事实并非如此。地球不仅在两极处变得扁平,而且其表面也是不规则的,因此我们采用大地水准面(Geoid)来描述地球真实轮廓,它是一个假想的由地球自由静止的海水平面扩展延伸而形成的闭合曲面,也是海拔高程系统的起算面。
大地水准面是真实地球表面的第一级逼近,这种方法的优点是非常接近自然地球的形状和大小,并且位置比较稳定。然而同样,大地水准面很难通过数学公式进行表达,为了计算与研究的方便,我们采用一个规则的参考椭球体来实现对大地水准面的数学逼近,如图2-4所示。
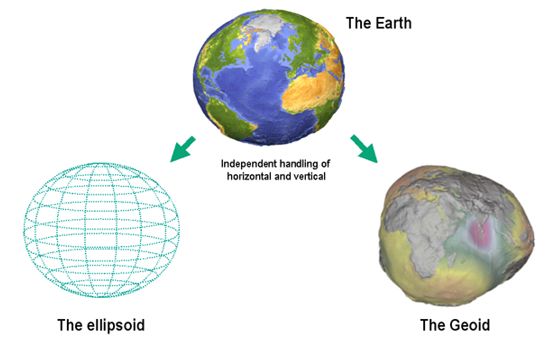
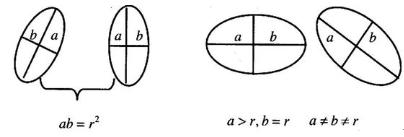
椭圆形状由两个半径定义。较长的半径称为长半轴,而较短的半径称为短半轴。将椭圆绕短半轴旋转即生成参考椭球体。图2-5显示了旋转椭球体的长半轴和短半轴。
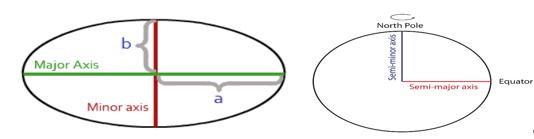
其中扁率
。当短半轴b减小时,扁率
增大,参考椭球体越扁,特殊情况
时变为二维平面,
时变为球体。
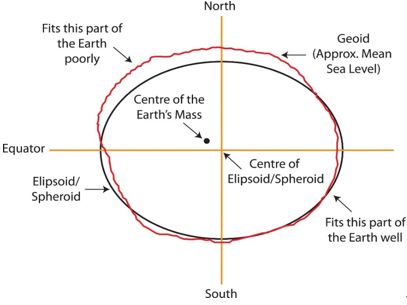
参考椭球体是真实地球表面的第二级逼近,为了以尽可能小的失真来表示大地水准面,我们尝试将其投影到参考椭球体上,包括适合世界特定地区的参考椭球体以及最适合全球大地水准面的参考椭球体。对于较小区域的高精度地图,其椭球体形状不容忽视。对于每个映射区域,可以仔细选择不同的参考椭球,以便最佳匹配大地水准面,从而匹配地形特征。图2-6表现出参考椭球在某些区域拟合大地水准面的效果最好,而在另外某些区域拟合效果最差。
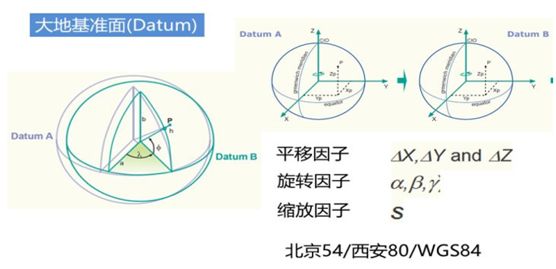
大地基准面是真实地球表面的第三级逼近,其通过控制参考椭球和地球的相对位置,从而尽可能与某一区域的大地水准面密合的一个椭球曲面。大地基准面是人为确定的,如图2-7所示。椭球面和水准面肯定不是完全贴合的,采用同一个椭球体,可以通过平移、旋转、缩放等操作去最大限度拟合不同的区域,因此同样的椭球体能定义不同的基准面,如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky椭球体,但它们的大地基准面显然是不同的。
总而言之,大地水准面是由假想的静止海水平面延伸而形成的连续、闭合曲面,唯一且不规则。规则的参考椭球体表面可以拟合大地水准面,与大地水准面是多对一的关系。而当采用同一个参考椭球体时,也可以通过选择不同的大地基准面来满足不同区域的实际需要。因此,大地水准面与参考椭球体是一对多的关系,参考椭球体与大地基准面也是一对多的关系,最终我们可以在大地基准面上建立地理坐标系来定量描述地球表面上每一个点的坐标。这也是进行地图投影的首要工作。
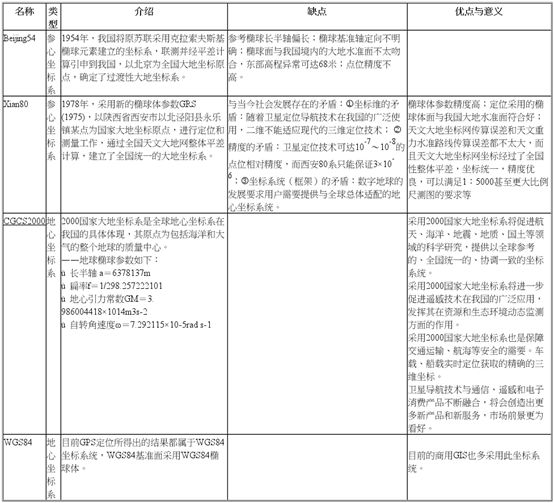
(4)中国采用的地理坐标系
通常所说的北京54坐标系、西安80坐标系是我国的两个大地基准面。我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了北京54坐标系,1978年采用国际大地测量协会推荐的1975地球椭球体(IAG75)建立了我国新的地理坐标系--西安80坐标系。北京54与西安80两者控制点坐标只能通过一定的数学模型,在一定精度范围内进行转换。北京54与西安80坐标之间的转换也可查阅国家测绘局公布的对照表。
WGS1984基准面采用WGS84椭球体,是以地心作为椭球体中心,是为GPS全球定位系统使用而建立的坐标系统。通过遍布世界的卫星观测站观测到的坐标建立 CGC2000国家大地坐标系是全球地心坐标系统在我国的具体体现, 采用的参考椭球非常接近WGS84,现今已将CGS2000坐标系作为测绘成果输出标准。图2-8介绍了中国各地理坐标系的优缺点与意义。
2
投影坐标系的定义
投影坐标系在二维平面中进行定义,通过格网上的x,y坐标来标识位置,其原点位于格网中心。每个位置均具有两个值,这两个值是相对于该中心位置的坐标。一个指定其水平位置,另一个指定其垂直位置。这两个值称为x坐标和y坐标。采用此标记法,原点坐标是x= 0和y = 0。
如图2-9所示,在等间隔水平线和垂直线的格网化网络中,中央水平线称为x轴,表示经度值,而中央垂直线称为y轴,表示纬度值。在x和y的整个范围内,单位保持不变且间隔相等。原点上方的水平线和原点右侧的垂直线具有正值;下方或左侧的线具有负值。四个象限分别表示正负x坐标和y坐标的四种可能组合。
三、地图投影方式
地球椭球表面是一种不可能展开的曲面,要把这样一个曲面表现到平面上,就会发生裂隙或褶皱。在投影面上,可运用经纬线的“拉伸”或“压缩”(通过数学手段)来加以避免,以便形成一幅完整的地图,如图3-1所示。
1
地图投影变形及参数
地图投影方式的选择即要求满足特定区域内的变形程度最小,因此本文先介绍地图投影中存在哪些变形。地图投影的变形通常有三种:长度变形、面积变形和角度变形。
长度变形:可以使用长度比μ来表示。长度比是指地面上的微分线段经过投影后的长度与原有长度的比值。值得注意的是,这与比例尺并非一个概念。长度比是一个变量,它随着在地图上位置的变化而变化。
面积变形:可以使用面积比Ρ来表示。面积比是指地面上的微分面积经过投影后的大小与原有大小的比值。面积比也是一个变量,如图3-2所示。
角度变形:是指地面上的任意两条线的夹角α与经过投影后的角α′的差,如图3-3所示。由于地面上的一点可以引出无穷条方向线,因此角度变形一般指最大角度变形。
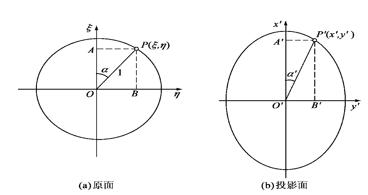
其中,各种变形相互联系相互影响:等积与等角互斥,等积投影角度变形大,等角投影面积变形大。实现等角、等面积、等距离同时做到的投影是不存在的。如图3-4所示,右上角为地球表面无变形的两幅人脸,图3-4左上部分的投影展开为扇形或矩形的地图无角度变形,其经纬线保持垂直关系,然而可以很明显的看出面积变形相当严重,人脸的面积放大了数倍;与此相对应的是图3-4的右下部分投影,人脸面积变化不大,然而经纬线的角度关系是不正确的,这也意味着图上任意两点的连线方向与真实情况存在很大的误差。
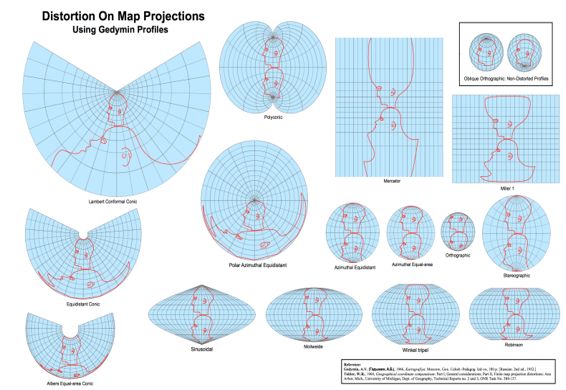
通常在应用中我们需要输入投影参数即标准线和中心线,用于确定投影的应用范围。如图3-5所示,标准线是投影面与参考椭球的切线或割线,分为标准纬线与标准经线,特点是没有变形,也称主比例尺;中心线是指中央经线(原点经线)与中央纬线(原点纬线),用来定义图投影的中心或者原点,特点是一般会有变形。
2
投影方式分类及特点
投影方式按变形分类可以分为等角投影,等积投影和任意投影。等角投影的角度变形为零(Mercator投影)。等积投影的面积变形为零(Albers投影)。任意投影的长度、角度和面积都存在变形。等角投影便于量测方向,故可应用于编制航海图、洋流图、风向图。等距投影,可用于对投影变形要求适中或区域较大的地图,如教学地图、科学参考图、世界地图。等积投影无面积变形,可在地图上进行面积对比与量测,故可应用于编制对面积精度要求较高的自然地图和社会经济地图,如地质图、土壤图、行政区划图。
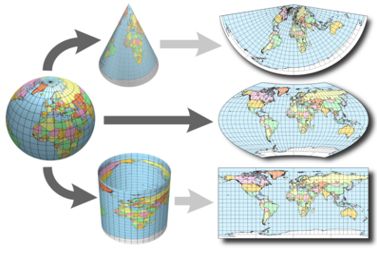
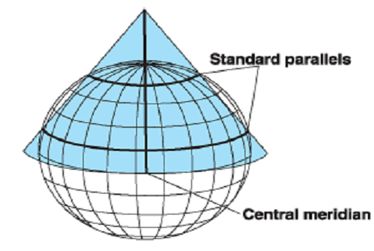
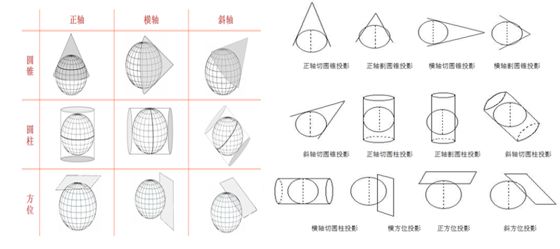
投影方式也可以按照投影面类型、投影面与地轴关系、投影面与地球表面关系分类。投影面有三种类型:圆柱、圆锥、平面(方位)。
投影面与地轴关系有三种类型:正轴、斜轴和横轴。正轴投影是投影面中心轴与地轴相互重合;斜轴投影是投影面中心轴与地轴斜向相交;横轴投影是投影面中心轴与地轴相互垂直。
投影面与椭球表面关系有两种类型:相切和相交。相切投影是投影面与椭球体相切;相割投影是投影面与椭球体相割。
如图3-6左图显示了考虑投影面类型和投影面与地轴关系的九种投影方式,右图显示了部分相切投影和相割投影。
在实际应用中投影方式经常采用发明者的名字而非投影分类的类型命名,因此我们需要了解某些特殊命名投影方式的投影性质,如图3-7所示。
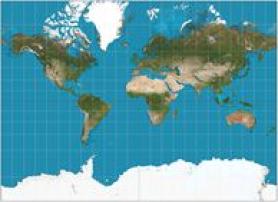
①墨卡托投影
正轴等角圆柱投影,经线和纬线是两组相互垂直的平行直线,经线间隔相等,纬线间隔由赤道向两级逐渐扩大。无角度变形,面积变形较大。该投影的等角航线为直线,这一特性对航海有重要意义,可用于编制航海地图,赤道附近国家及一些区域的地图。
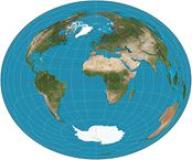
②兰伯特投影
横轴等积方位投影,赤道和中央经线为相互正交的直线,纬线为凸向并对称于赤道的曲线,经线为凹向并对称于中央经线的曲线。可用于编制东、西半球地图。右图为球面投影,横轴等角方位投影,视点在球面,切点在赤道的完全透视的方位投影。
③博斯特尔投影
正轴等距方位投影,纬线为同心圆,经线为交于圆心的放射状直线,其夹角等于相应的经差。特点:经线方向上没有长度变形,因此纬线间距与实地相等;切点在极点,为无变形点;有角度变形和面积变形,等变形线均以极点为中心,呈同心圆分布,离无变形点愈远,变形愈大。可用于编制南、北半球地图和北极、南极区域地图。联合国即采用这种地图图案制作联合国会徽。
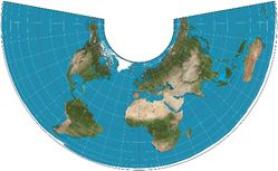
④亚尔勃斯投影
正轴等积圆锥投影。可用于编制全国性自然地图中的各类分布图、类型图、区划图以及全国性社会经济地图中的行政区划图、人口密度图、土地利用图。
⑤高斯-克吕格投影
横轴等角切椭圆柱投影,中央经线与赤道垂直,经线为凹向并对称于中央经线的曲线,纬线为凸向并对称于赤道的曲线,经纬线成直角相交,分为6度和3度带分带投影。大于1:1万的地形图采用3度带投影,1:2.5万至1:50万的地形图采用6度带投影。


(6)高斯-克吕格投影
图3-7 某些投影方式及其特点
3
投影选择实例
投影方式有多种多样,一个国家或地区依据自己所处在的经纬度、幅员大小以及图件用途选择投影方式。在大于1:10万的大比例尺图件中,各种投影带来的变形可以忽略。选择地图投影时,主要考虑制图区域的范围、形状和地理位置(主要因素)、地图的用途、出版方式及其他特殊要求。
(1)世界范围内投影方式
世界地图,主要采用正圆柱、伪圆柱和多圆锥投影。在编绘世界航线图、世界交通图与世界时区图时也采用墨卡托投影。中国出版的世界地图多采用等差分纬线多圆锥投影。
对于半球地图,东、西半球图常选用横轴方位投影;南、北半球图常选用正轴方位投影;水、陆半球图一般选用斜轴方位投影。在东西延伸的中纬度地区,一般采用正轴圆锥投影,如中国与美国。在南北方向延伸的地区,一般采用横轴圆柱投影或多圆锥投影,如智利与阿根廷。
(2)中国范围内投影方式
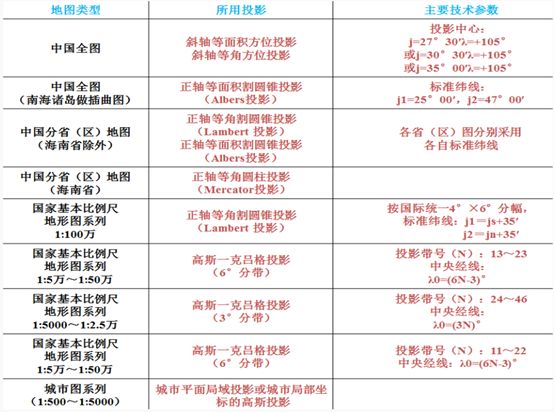
①我国基本比例尺地形图(1:100万、1:50万、1:25万、1:10万、1:5万、1:2.5万、1:1万、1:5000)除1:100万以外均采用高斯-克吕格Gauss-Kruger投影(横轴等角切圆柱投影,又叫横轴墨卡托Transverse Mercator投影)为地理基础。
此种投影方式的特点是离中央子午线越远,变形越大。投影后赤道是一条直线,赤道与中央子午线保持正交。离开赤道的纬线是弧线,凸向赤道;没有角度变形,长度和面积变形很小。北京54和西安80投影坐标系即采用了这种投影方式。
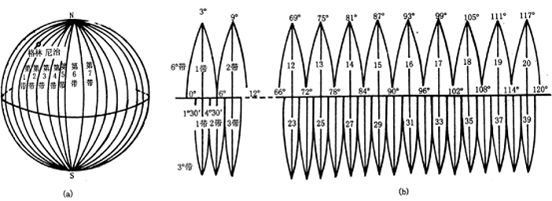
因为在纬线方向上长度变形过快,高斯克吕格投影采用分带的方式控制投影变形。即每隔一定的经度重新确立一条新的中央经线,保证在这个经度范围内的长度变形保持可接受的精度,共有6°分带和3°分带两种方式。如图3-8所示。
6°分带 用于1:2.5万 -1:50万比例尺地图起始于本初子午线(格林威治),按经差6度为一个投影带自西向东划分,全球共分60个投影带。我国范围可分成11个6度带(第13号带到第23号带)。
3°分带用于大于1:1万比例尺地图始于东经1°30′,按经差3度为一个投影带自西向东划分,全球共分120个投影带。我国范围可分成22个三度带(第24号带到45号带)。坐标系原点为每个投影带的中央经线与赤道交点。
②1:100万地形图采用兰伯特Lambert投影(正轴等角割圆锥投影),其分幅原则与国际地理学会规定的全球统一使用的国际百万分之一地图投影保持一致。
③海上小于50万的地形图多用墨卡托Mercator投影,即正轴等角圆柱投影。
④我国大部份省区图以及大多数这一比例尺的地图也多采用兰伯特投影和属于同一投影系统的Albers投影(正轴等积割圆锥投影)。
中国常用地图投影如图3-9所示。
四、地图投影的有趣应用
1
两点之间的最短路径是什么?
假设我们需要计划两个遥远点之间的旅程行程,如坎皮纳斯(巴西东南部)和东京(日本)。假设我们可以乘飞机旅行,并简化忽略应当避免的事情,例如恶劣的天气和受限制的空域。显然,我们希望通过选择最短的路线来减少时间和成本,这种路线在平坦的表面上始终是一条简单的直线。那么,我们如何确定自己的道路呢?只需拿起一把尺子和一张地图,然后绘制一条线来加入我们旅程的终点?它不是那么简单,如果我们想要有意义的结果,选择正确的投影是必不可少的。
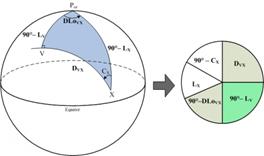
给定A和B两个点,如东京和坎皮纳斯,加上地球的中心,一个独特的(除非地心过AB组成的直线)平面被定义。这个平面与地球表面的交点是大圆,因为在包含A和B的圆中它是最大的,其半径和周长与地球相同;此时我们定义由包含地心的平面产生的任何表面圆都是一个大圆,任何不包含地心的表面圆都是一个小圆。因此,每条经线都是一个大圆,而除了赤道以外的所有纬线都是小圆。如图4-2所示,PX可以看做是P和X两点的大圆弧,而PV和VX不在两点间的大圆弧上,由三角形的定理可知,两边之和大于第三边,即PV+VX>PX,因此大圆才是球面上两点的最短路径,而不是两点的直线。
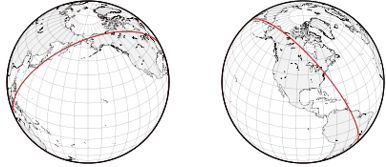
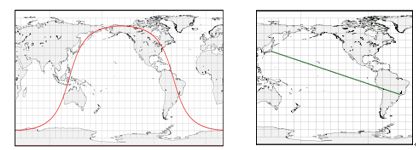
因此,从巴西到日本的最短路径如图4-3红线所示,从上方两图可以看到从球面路线来看,经由美国东海岸与阿拉斯加到达东京才是最短路径,但在地图投影中则是一条相当弯曲的弧线。简单地将巴西和日本投影在等距圆柱形地图上的直线相连(绿线)可能会得出天真的结论,即夏威夷比阿拉斯加更适合转机。
2
动物学分类的世界地图
由于气候是动物群特征的重要决定因素,因此动物活动的大多数区域边界都遵循纬度,因此使用极坐标系星型投影是一种非常直观的方式。如图4-4所示。
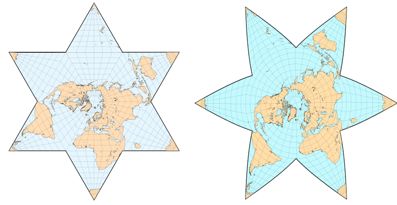
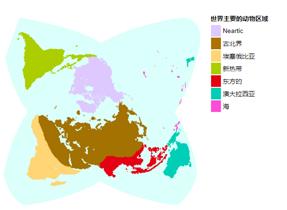
在地球的北半球,大陆地区聚集在极地周围,而赤道以南的广阔海域将稀疏的大陆分开; 此外,非洲和美洲向南缩小。地球上奇特的大陆分布是我们采用以北极为中心的中断星形地图投影的基础,以一个圆形核心(通常是一个半球)被裂片包围的形式表现,其中不太重要的南极洲在星型的末端分开成为几个不相连的部分。也有与此对应的反转模式,以南极地区为中心的星型地图研究海洋特征。Oliver L. Austin和Arthur Singer在1968年的世界鸟类研究中即采取了基于Maurer的星形投影地图(不包含南极洲),如图4-5所示。
五、总结与展望
地图制图的优劣表达了我们是否能准确认识我们所居住的这个星球。从古代的天圆地方到如今纤毫可见的卫星地图,这正是我们对世界的认识不断加深的过程。而地图投影的选择是否恰当,直接影响地图的精度和实用价值。因此在制图以前,要根据各种投影的性质、经纬网的形状特点,然后结合制图区域的形状和地理位置、制图区域的范围、地图的内容和用途以及出版方式,科学的选择地图投影,避免犯“南辕北辙”的错误。
来源:测绘学术资讯
原标题:《科普 | 同一个世界,地图有这么多不同的表达!》
