原创 谭景芳 王成会 等 物理与工程

摘要

本文在双节拍器耦合系统动力学方程的基础上，利用Runge-Kutta（龙格库塔）法对振动系统进行数值分析，通过摆杆摆角随时间演化的曲线图像，讨论影响系统同步性质的因素。利用L-P（林德斯泰特庞加莱）法研究相同双节拍器耦合系统的系统参数对于摆杆摆动振幅和摆动频率的影响，得到无耦合双节拍器系统的近似解，结合数值分析比较系统参数对同步周期和振幅的影响；在理论分析得到的近似同步周期中设定同步系数q值，并通过拟合函数进行拟合，拟合后得到的同步周期与数值分析的周期基本一致。本文能为更好地理解耦合系统的同步性质提供参考，也能为学生进行双节拍器同步物理实验提供一些理论参考, 增强学生理论联系实际的能力。

关键词耦合同步；振动系统；频率响应RESEARCH ON SYNCHRONIZATION OF DOUBLE METRONOME

COUPLING SYSTEM BASED ON LINDSTEDT-POINCAR METHODTAN JingfangWANG ChenghuiMO Runyang

(School of Physics and information Technology, Shaanxi Normal University, Xian, Shaanxi 710119)

AbstractIn this paper, we used dynamics equation of the coupled system of double metronome to analyze the vibration system numerically by Runge-Kutta method, and discussed the factors affecting the synchronization of the system by using the curve image of the pendulum angle evolution with time. L-P (Lindstedt-Poincare) method was used to study the influence of system parameters of the same double metronome coupling system on the pendulum amplitude and frequency, and obtained the approximate solution of the uncoupled double metronome system, compared with numerical analysis to discuss the effects of system parameters on synchronization period and amplitude. The approximate synchronization period is obtained by theoretical analysis, we set q as synchronization coefficient, and used fitting function to fit q value. After fitting, the synchronization period is basically consistent with the period of numerical analysis. This paper can provide a reference for better understanding the synchronization properties of coupled systems, and also provide some theoretical references for students to conduct the physical experiment of double metronome synchronization，enhance students ability to combine theory with practice.

Key wordssynchronization coupling；vibration system；frequency response

自然界有很多同步现象[1,2]，如萤火虫间的同步闪烁、行星对卫星的潮汐锁定、神经元间的同步放电等；同步激励振动的应用方面有振动筛、航天工业等。弱耦合的多振子模型一般为Kuramoto 模型[3-6]。双振子模型简单且包含着多振子耦合同步的基本特性，即振子间互相耦合，相互影响，因此研究双振子的同步行为便于更好地理解多振子的同步行为。节拍器耦合同步实验[2]是常用于研究的双振子模型，其同步现象是比较经典的同步现象之一，研究振子耦合问题对于解决自然界的同步行为有重要的帮助。

文献[7]给出了多节拍器耦合的力学模型并通过质心系的动量矩和动量定理得到多节拍器耦合的动力学方程，然后通过数值仿真模拟出了双节拍器和三节拍器的耦合时间；文献[8]分析了单个节拍器摆动的物理图像，然后分析了双节拍器同步和反向同步的现象。文献[9]分析了双节拍器耦合的原因，开始时不同步会使各个节拍器在每次摆动都收到一次微弱冲击，造成节拍器相位的微小改变，多次冲击使得两节拍器间相位差为零或π时，此时双节拍器达到同步。文献[10]探究了不对称节拍器耦合系统的同步行为，将同平面的双节拍器耦合系统推广至上下两层，通过在一层节拍器产生节拍信号的位置放上一张纸，使得信号的强度发生变化，从而可以从音频信号上分开上下层信号，达到对双层节拍器耦合进行分析的目的；通过改变双层之间、底座与桌面之间摩擦力数值模拟相流，研究不同的同步模式中摆角的分布范围。单节拍器的摆动方程可以转化为杜芬方程，文献[11]利用久期微扰理论通过试探解将二阶耦合的杜芬方程转化了一阶耦合的杜芬方程，文献[12]则在此基础上通过表象变换，将一阶耦合的杜芬方程进行解耦，得到了模式解，但耦合项为线性项，不符合双节拍器耦合系统。上述研究中，系统参数对耦合同步性质的影响研究不彻底，也没有从理论方面给出双节拍器系统的同步周期。

由于系统参数对摆杆的摆动振幅和摆动频率的影响的定性分析研究较少，本文基于双节拍器耦合系统的动力学模型，利用 L-P法得到双节拍器耦合系统的近似解，通过理论分析和数值分析研究系统参数对两摆杆同步时摆动振幅和摆动频率的影响，理论分析得到的同步周期近似解能够较好地反映同步周期的变化特征；引入同步系数 q 值，通过理论分析得到的拟合函数对同步系数进行修正，能较好地给出相同的双节拍器耦合系统的同步周期。

1 数学模型与理论分析

节拍器能周期稳定地发出“滴答”的声音来记录节拍，其根据钟摆原理制成，摆锤会周期性摆动，因此可以将一个节拍器简化为一个摆锤做单摆运动的模型。

在一个平面上架上两个滚轮，在滚轮上水平放置一个平板，滚轮的纵轴向与平板其中的一个轴向平行，在平板上方同一平面上相距一定距离放置两个节拍器,节拍器摆动方向要与平板移动方向一致，就构成了一个双节拍器耦合系统，简化模型如图1所示。

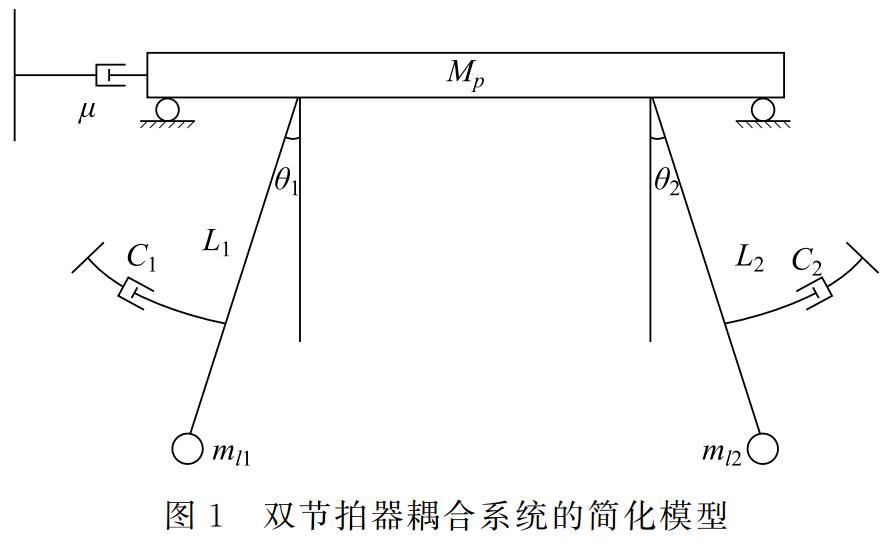
由动量定理和动力矩定理可得节拍器耦合系统动力学方程组[7]

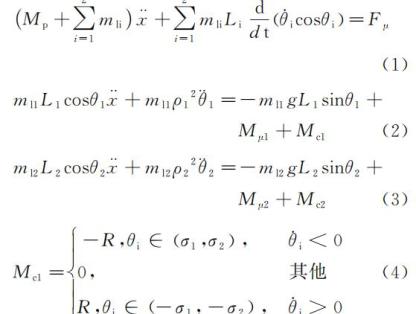
其中, mli 为第i个摆杆的质量，Mp 为平板和双节拍器底座的质量，Lli 为第 i 个摆杆质心到悬挂点的距离，θi 为第 i 个摆杆与铅垂线的夹角，ρi为回转半径，σ1和σ2为驱动力矩的摆角范围，Mci为第 i 个节拍器的擒纵机构对摆杆施加的驱动力矩。其中 Mμi为第i个摆杆受到的阻尼力矩，Fμ为地面对木板产生的摩擦力，Ii 为第i个摆杆的转动惯量，其分别为形式为

，μ 为地面与滚轮间的摩擦力系数，Ci 为阻尼系数，R 为驱动力矩大小。式(1)~(3)一个耦合项为非线性项的二阶微分方程组。通过摄动法对木板的质心位移进行线性化求解，对式(1)，令

， 有

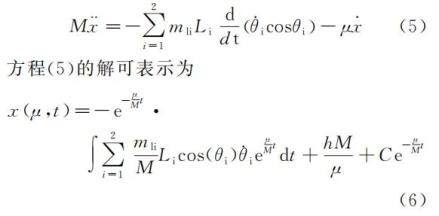
其中，h，C为常数，式(6)的初始条件表示为

。若系统摩擦系数 μ=0，则方程(1)的解退化为

其中，a，b 为积分常数，由初始条件表示为

决定。在摩擦系数很小的情况下，有 μ→0时，若式(7)减去式(6)，有

因此，可用正则摄动问题讨论微分方程(1)的解，由正则摄动法得到的解近似表示原系统方程(1)的解。根据摄动法，对x进行 Taylor展开，有

保留 μ 的一次项，代入方程(1)，得

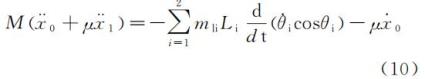
对方程(10)积分，有

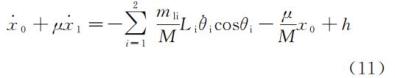
其中，h 为积分常数，可由系统初始条件决定；继续考虑式(10)中含 μ 的一阶项，则一阶近似解满足的方程可表示为

联立式(11)和式(12)可得木板的位移与双节拍器摆杆摆角的关系对应的近似解为

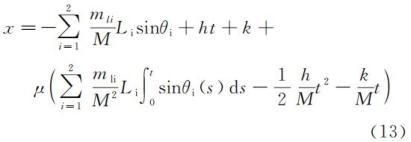
式(13)给出了木板的位移与双节拍器摆杆摆角的关系，因此，将其求二阶导后忽略其中含 μ 的高阶小量项，则木板的加速度可近似表示为

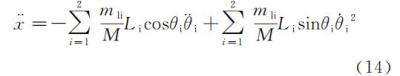
将式(14)代入式(2)(3)，化简可得节拍器摆杆摆角满足的二阶微分方程为

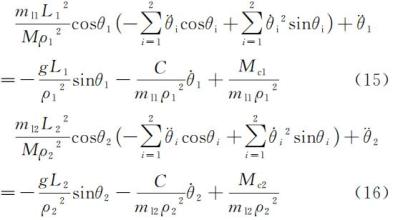
由于方程(15)和(16)中含系数

的项远小于其他项，故可将其项视作扰动项。由 L-P 法，令小量

以及 τi=ωit，则

，故有

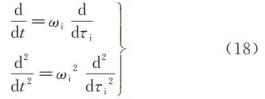
将式(18)代入式(15)及式(16)，且令sinθ10=q1θ10，sinθ20=q2θ20，仅考虑两个节拍器相同的情形，比较得到零阶项为

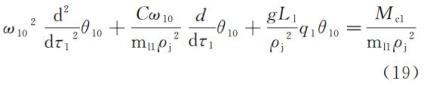
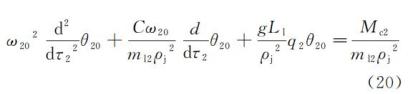
其中，q1，q2 为同步系数。方程(19)和(20)即为耦合系统方程(1)~(3)经过解耦处理后无耦合项扰动的单摆模型。其中 Mc1，Mc2 为驱动力。令 ωi0=1，

，设 P 和 Q 的傅里叶级数展开式为

其中 vi，ti，kj，dj 为傅里叶系数，ω1+，ω2+ 为摆杆摆角圆频率。为简化分析，主要考虑 i=j=1 的驱动力函数作用，此时，式(19)(20)的通解为

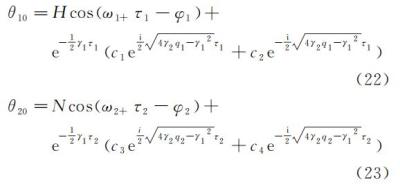
其中，c1、c2、c3、c4是与初始条件相关的积分常数。引入

，

，其中 β1、β2、δ1、δ2 为

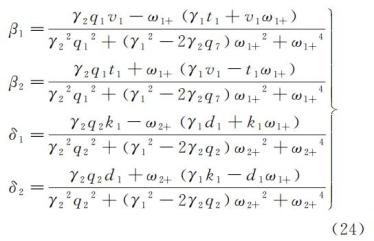
由式(22)(23)可知无耦合项扰动的自由单摆模型的主要频率项为

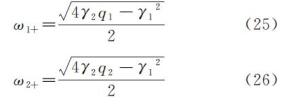
方程(25)(26)表明耦合系统的摆动频率主要受系统的阻尼系数、摆杆的转动惯量、摆杆质心到悬挂点的距离这些参数影响。由式(22)(23)可知，

中衰减系数 γ1 越大，振子摆动的振幅衰减得越快，而 γ1 与阻尼系数、摆杆的转动惯量有关，故系统的阻尼系数越大，摆杆的转动惯量越小，振子摆动衰减越快。当经过较长时间后，右边的第二项衰减为零；第一项代表摆杆在稳定同步时摆角的变化规律，是摆动为振幅和频率相关的正弦函数形式。结合式 (25)(26)，可见振子振幅和频率的变化与阻尼系数、摆杆的转动惯量有关，其改变将影响耦合系统的同步特性对摆动振幅与摆动频率的敏感性。

2 耦合系统动力学的数值模拟

本节通过四阶龙格库塔法对双节拍器耦合同步方程组(1)~(3)进行数值分析，双节拍器耦合系统的动力学方程中系数设为MP=1kg，mli=0.1kg，ρl=18mm，Ll=7.5mm，g=9.98m/s2，σ2=0.2rad，σ1=0.1rad, Ci=3.0×10－5N·m·s/rad，μ=1.0×10－3N·s/m，R=3.5N·mm。

2.1 摆角的数值模拟

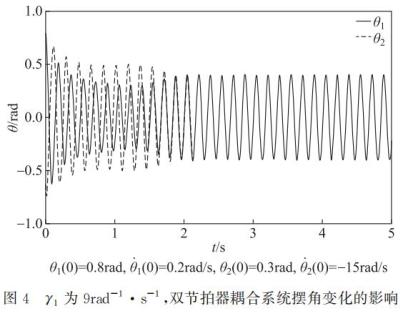
随着系统的演化，一个摆杆不断通过平板质心运动影响着另一个摆杆的摆动，同时也受到另一个摆杆的摆动影响，经过多次弱耦合作用后，节拍器最终可达到同相（或反相或延迟）同步状态，此时两摆杆摆角的差值趋于定值。数值分析结果表明：无论在哪种同步状态下，系统的摆动周期保持不变。图 2 给出了不同的初始条件情形下两摆角的同步演化规律，发现达到同步所需要的时间与初始条件密切相关；在耦合过程中，摆杆摆角的变化具有正弦函数变化特征；同相同步时，摆杆摆动振幅约为 0.69rad，摆动周期约为 0.416s，并且反相同步时也能保持相同振幅和周期，因此，同步后摆杆振幅和周期只与系统参数有关，与初始条件无关。两摆杆摆角的相位差如图 3 所示，表现为先增大后减小并最终稳定为幅值为 0.007rad、周期为 0.416s 微小扰动变化，此时系统处于同步状态，摆角的相位差值最终的变化周期与摆角的同步周期几乎一致，因此可以以摆角的差值的稳定来判断系统是否达到同步。比较图 2（a）与图 4 发现，当 γ1 值从 0.857rad－1·s－1增大至 9rad－1·s－1时，系统达到同步所需的时间从大约 9s 变为约 3s，摆杆的摆动振幅变化更快，这与近似理论关系式(22)和式(23)预测结果一致。

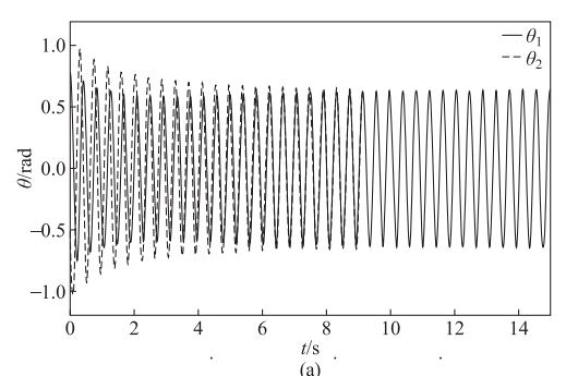
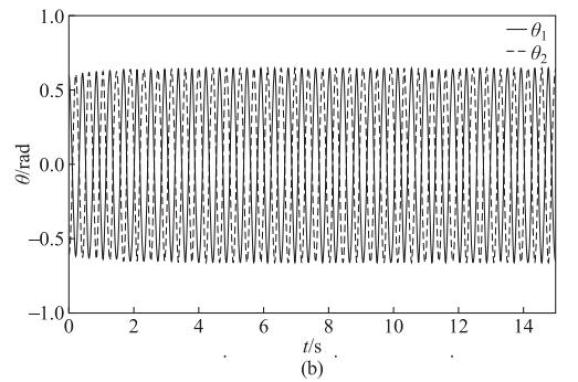
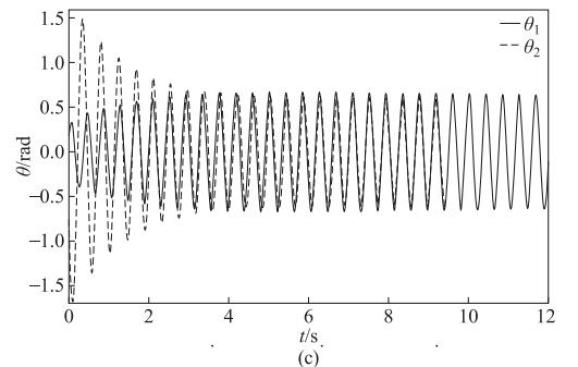
图 2 不同初始条件下对双节拍器耦合系统摆动行为的影响

(a)θ1(0)=0.8rad,θ1(0)=0.2rad/s,θ2(0)=0.3rad,θ2(0)=－15rad/s；(b) θ1(0)=0.6rad,1(0)=0rad/s,θ2(0)=－0.6rad,θ2(0)=0rad/s；(c) θ1(0)=0.2rad,θ1(0)=4rad/s,θ2(0)=－0.8rad,θ2(0)=－20rad/s

2.2 同步周期的拟合

通过数值分析得到的摆角随时间演化曲线可观察系统达到同步状态的过程以及获得同步振动周期和振幅等参量。当系统处于稳定同步状态时，可认为同步后的摆角演化曲线上连续两个峰的峰值所对应的时间差作为一个周期。为更精确地量度同步周期，可在曲线上随机取三个不同位置处的峰值对应时间差分别表示为T1，T2，T3，取这三个时间差的平均值作为数值计算的同步周期，即

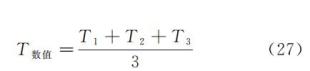
由式(25)和式(26)，可得相同节拍器组成的双摆系统的同步周期的理论近似值为

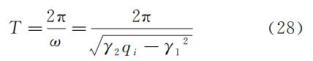
当

时，式(28)可表示为

式(29)说明系统参数满足

时，摆杆的同步周期与回转半径成正比。令同步系数 q1=q2=1，即在实现同步后对摆角取线性近似，则通过控制变量法，改变其中一个系统参数，比较不同摆长、摆杆质量、回转半径下同步周期的近似理论值与数值解， 如表 1~表 3 所示。对比发现，在给定的同步系数下，部分摆长对同步周期的理论值与数值解之间的相对误差影响较大，当摆长从2mm 变化到 15mm 时，同步周期减小，相对误差值有正有负，因此，近似理论值和数值解之间的差异不具备一致性（表1）。当摆杆质量从 0.05kg 变化到 0.3kg 时，同步周期无论是理论值还是数值解，差异小于 0.007s，若以 0.41s作为偏移基准，则偏移量小于 1%，因此，我们可以认为摆杆质量对同步周期的影响不大（表2）。从回转半径分析结果看（表3），近似理论中，回转半径与同步周期近似成正比关系，这与式(29)的分析一致。因此，通过不同摆长、摆杆质量和回转半径的同步周期理论值与数值解的结果比较，发现式(28)给出的近似理论式能够较好地反映同步周期的变化特征。对于表 1~3 中部分摆杆同步周期的理论值与数值值二者间的差异过大，我们认为主要与 q 值的选取有关。

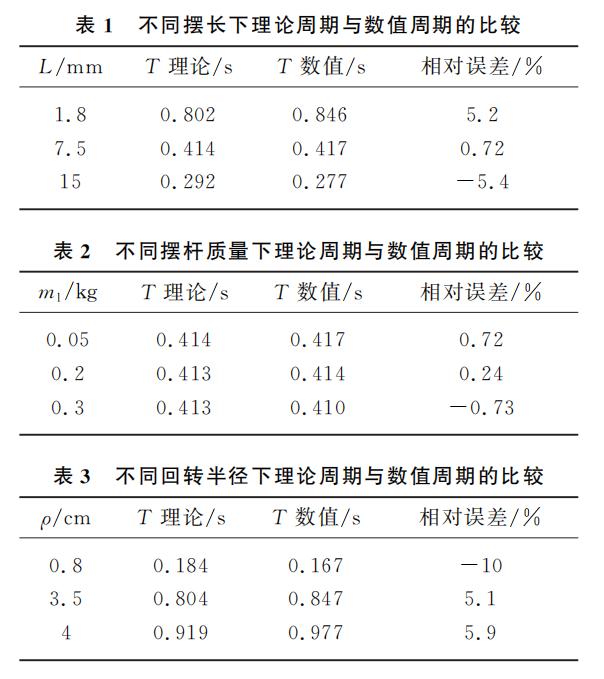
因 q 值可影响同步摆动周期，为缩小数值解与理论近似值之间的差异，且更好地观察系统同步过程中摆角近似理论分析时对 q 值的依赖，联立式(27)和式(28)，q 值可近似表示为

我们可以通过从数值解与理论近似分析对照得到 q 值代入到式(28)，进一步修正系统达到同步后的摆动周期理论表达式。设拟合函数为

其中，a,b,c 为待定参数。取摆杆的摆长从 2~70mm 不等间隔变化，质量从 0.05~0.6kg 不等间隔变化，回转半径从 4~50mm不等间隔变化，其他系统参数为MP=1kg，g=9.98m/s2，σ2=0.2rad，σ1=0.1rad，μ=1.0×10－3N·s/m，Ci=3.0×10－5N·m·s/rad， R=3.5N·mm 时，通过数值解确定 γ12 和 γ2，然后通过数值分析得到同步周期，进而得到q值。通过一系列的 γ12、γ2 和 q 值对拟合函数(31)进行数值分析， 从而可得待定参数 a,b,c 的取值为

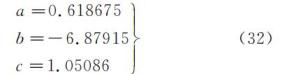
将式(32)代入式(31)可得到修正的 q 值，将其代入式(28)可实现对同步周期理论近似表达式的进一步修正。根据修正后的 q 值取新的同步参数，再次将修正后的同步周期理论式得到的近似值与数值解进行对照，分析得到的同步周期相对误差的绝对值小于 5%，表明拟合后的理论周期与数值周期相符的较好，说明式(28)能较好地给出相同的双节拍器耦合系统的同步周期。

3 结语

本文在相同双节拍器动力学模型的基础上，通过数值分析发现，摆杆摆角随时间的演化具有正（余）弦函数变化特征，初始条件会影响两摆杆达到同步所需要的时间和最终的同步状态，当两摆杆同步后，摆杆振幅和周期保持不变，且振幅和周期只与系统参数有关，与初始条件无关。通过L-P法对双节拍器耦合系统的动力学方程进行解耦，得到用无耦合单摆模型表示的近似解，发现系统达到同步时的摆动周期主要受系统的阻尼系数、摆杆的质量、回转半径、摆长影响；阻尼系数越大，转动惯量越小，系统摆杆摆动振幅变化得越快，阻尼系数、摆杆的转动惯量的改变会影响耦合系统的同步特性对摆动振幅与摆动频率的敏感性。最后对理论分析得到的近似同步周期进行讨论，结合数值分析，发现理论近似式能够较好地反映同步周期的变化特征；通过理论分析得到的拟合函数对同步系数 q 值的修正，当摆杆的质量、回转半径、摆长变化时，其同步周期与理论推导得到的周期大致符合，误差的绝对值小于 5%。

参考文献

[1]ZHOU Z S, KURTHS J, ARENAS A, et al. Synchronization in Complex Networks[D]. New York: Springer Theses, 2016.

[2]FOSTER R G, KREITZMAN L. The Rhythms of Life[M]. New Jersey: Princeton University Press, 200: 10.

[3]KURAMOTO Y. Self-entrainment of a population of coupled non-linear oscillators[J]. Lecture Notes in Physics, 1975, 39: 420-422.

[4]王学彬, 徐灿, 郑志刚. 多重耦合振子系统的同步动力学[J]. 物理学报, 2020, 69(17): 31-42.

WANG X B, XU C, ZHENG Z G. Synchronization dynamics of multiple coupled vibration subsystems[J]. Acta Physica Sinica, 2020, 69(17): 31-42.（in Chinese）

[5]YU D, YANG J Z. Effects of Correlation between Network Structure and Dynamics of Oscillators on Synchronization Transition in a Kuramoto Model on Scale-Free Networks[J]. Communications in Theoretical Physics, 2014, 02: 197-202.

[6]ERNEST M, DIEGO P. Kuramoto Model for Excitation-Inhibition-Based Oscillations[J]．Physical Review Letters, 2018, 120(24): 244101.1-244101.6

[7]王晓军, 吕敬, 王琪. 多节拍器耦合系统的动力学建模与分析——动量(矩)定理的应用[J]. 力学与实践, 2017(6)：606-609.

WANG X J, LV J, WANG Q. Dynamic Modeling and Analysis of Multi-metronome Coupling Systems—Application of momentum (Moment) Theorem[J]. Mechanics in Engineering, 2017(6): 606-609.（in Chinese）

[8]金山, 吕建锋. 平行摆放的节拍器相互耦合的动力学机制[J]. 大学物理, 2018(8): 47-53.

JIN S, LV J F. The dynamics of the coupling of parallel metronomes[J]. College Physics, 2018(8): 47-53.（in Chinese）

[9]路峻岭, 顾晨, 秦联华, 等. 关于多个节拍器自锁同步实验的探究[J]. 大学物理, 2018, 37(9): 25-29.

LU J L, GU C, QIN L H, et al. Research on the self-locking synchronization experiment of multiple metronomes[J]. College Physics, 2018, 37(9): 25-29.（in Chinese）

[10]ZHANG J, YU Y Z, WANG X G. Synchronization of coupled metronomes on two layers[J]. Frontiers of Physics, 2017, 12(6): 53-62.

[11]朱存远, 李朝刚, 方泉, 等. 用久期微扰理论将弹簧振子模型退化为耦合模理论[J]. 物理学报, 2020(7): 120-126.

ZHU C Y, LI C G, FANG Q, et al. The spring oscillator model degenerated into the coupled-mode theory by using secular perturbation theory[J]. Acta Physica Sinica, 2020(7)：120-126.（in Chinese）

[12]李朝刚, 汪茂胜, 方泉, 等. 表象变换和久期微扰理论在耦合杜芬方程中的应用[J]. 物理学报, 2021(2): 353-359.

LI C G, WANG M S, FANG Q, et al. Applications of representation transformation and secular perturbation theory to coupled Duffing equations[J]. Acta Physica Sinica, 2021(2): 353-359.（in Chinese）

基金项目: 教育部高等学校物理学类专业教学指导委员会项目“师范专业认证背景下基于OBE理念的力学课程教学模式研究”（2018-ZDGH-201），师范专业认证背景下师范院校教师教育课程设置研究（JSJY2021019），陕西师范大学课程思政示范课建设项目“理论力学”。

通讯作者: 王成会，女，陕西师范大学教授，主要从事超声空化和复杂介质内的声传播的理论分析、声场分布模型建立及其应用研究工作，研究方向为声学，Wangld001@snnu.edu.cn。

引文格式: 谭景芳，王成会，莫润阳. 基于林德斯泰特庞加莱法的双节拍器耦合系统同步规律研究[J]. 物理与工程，2023，33（5）：46-52.

Cite this article: TAN J F, WANG C H, MO R Y. Research on synchronization of double metronome coupling system based on Lindstedt-Poincaré method[J]. Physics and Engineering, 2023， 33（5）：46-52. (in Chinese)

END

更多精彩文章请点击下面“蓝字”标题查看：

CALL FOR PAPERS｜《物理与工程》征稿量子世纪年中国大学物理教育MOOC联盟2023年工作会议（扩大）暨典型案例交流会 会议纪要2023年全国高等学校物理基础课程教育学术研讨会 会议纪要2023 年全国高等学校物理基础课程青年教师讲课比赛在喀什大学举办全国大学物理实验教学对口支援（智力援疆）研讨会在新疆师范大学举办王青教授：理解王中林院士“拓展的麦克斯韦方程组”“碰瓷”麦克斯韦：伽利略协变和洛伦兹协变电磁场论趣谈热点：运动介质洛伦兹协变电磁理论2021年《物理与工程》优秀论文、优秀审稿专家、优秀青年学者名单王青教授：源自苏格拉底的问题驱动式教育——在互动中共同学习和成长读后感：教育中的现实和远方王青教授：昨晚（6月9日），清华电动力学期末考试朱邦芬院士：“减负”误区及我国科学教育面临的挑战《物理与工程》2023年第4期目录乐永康：新冠肺炎疫情防控下美国物理实验教学及中美情况对比顾牡：对于重新制定的《非物理类理工学科大学物理课程教学基本要求》的认识和体会朱邦芬院士：从基础科学班到清华学堂物理班朱邦芬院士：对培养一流拔尖创新人才的思考李学潜教授：物理是一种文化李学潜教授：如何帮助物理系学生迈过从高三到大一这个坎穆良柱：物理课程思政教育的核心是科学认知能力培养穆良柱：什么是物理及物理文化？穆良柱：什么是ETA物理认知模型穆良柱：什么是ETA物理教学法吴国祯教授：我的国外研究生经历印象——应清华大学物理系“基科班20年·学堂班10年纪念活动”而写

陈佳洱，赵凯华，王殖东：面向21世纪，急待重建我国的工科物理教育王亚愚教授：清华物理系本科人才培养理念与实践葛惟昆教授：关于中外人才培养的几点思考安宇教授：为什么传统的课堂讲授模式需要改变安宇教授：其实教学就是积累的过程刘玉鑫教授：关于本科生物理基础课程教学和教材编著的一些思考沈乾若：重创理科教育的美加课程改革Henderson C：美国研究基金支持下的物理教育研究及其对高等物理教育的影响《物理与工程》期刊是专注于物理教育教学研究的学术期刊，是中国科技核心期刊，1981年创刊，欢迎踊跃投稿，期刊投审稿采编平台：

http://gkwl.cbpt.cnki.net

欢迎关注

《物理与工程》微信公众号

继续滑动看下一个轻触阅读原文

物理与工程向上滑动看下一个

原标题：《基于林德斯泰特-庞加莱法的双节拍器耦合系统同步规律研究》