原创 李亚楠 张睿 物理与工程
摘 要
建设高质量教育评价体系是国家的政策导向和重点要求。作为教育评价体系的重要环节,学习预警可以帮助学生和教师及时了解学情,调整教学与学习策略,真正做到以学为中心的教学方式。本文根据大学物理混合式教学数据建立结构方程模型,将教学数据分为行为投入和认知投入两类,并通过主成分分析对学习投入进行测算。在学习投入模型的基础上,本文构建了学习效果评价方式,并进一步探讨了不同预警模型的性能。从结果上看,决策树 C5.0 构建的学习预警模型召回率等指标优于决策树 CART、线性回归、支持向量机以及 K-means 算法构建的学习预警模型,能更好地预测学生是否及格。
关键词 学习预警;混合式教学;学习投入;结构方程模型
Abstract Building a high-quality education evaluation system is a national policy guide and key requirement. As an important part of the education evaluation system, early-warning for learning can help students and teachers to know the situation in time, adjust teaching and learning strategies, and truly achieve a learning-centered teaching method. Based on the data of mixed teaching of college physics, this paper establishes a structural equation model, divides the data into behavioral engagement and cognitive engagement, and measures the learning engagement through principal component analysis. Based on the learning engagement model, we construct a learning effect evaluation method and further explores the performance of different early-warning models. According to the result, the recall rate of the learning early-warning model constructed by decision tree C5.0 is better than the learning early-warning model constructed by decision tree CART, linear regression, Support Vector Machine (SVM) and K-means algorithm, which can better predict whether students will pass or not.
随着互联网、大数据及机器学习的发展,信息技术与教育深度融合,教育技术的发展也与时俱进。其中混合式教学的理念受到了教育技术研究者的广泛关注,混合式教学为线上线下相结合的学习提供了平台,学生在学习过程中产生了大量的混合式学习数据,这些混合式学习数据可以反映出学生的学习投入,大量研究表明,我们可以从学生学习投入度的角度衡量学生学习成就,从而对学生进行学习预警,及早地向具有学习风险的学生发出预警信号,可以使教师及时调整教学策略、优化教学模式,使学生提高学习效果。
构建学习预警模型需要科学的教育评价体系,建设高质量的教育评价体系一直是党和政府的重点要求[1]。据教育部统计 2019 年全国各类高等教育在学总规模达 4002 万人,高等教育毛入学率达到 51.6%,高等教育迈入普及化发展阶段[2]。随着招生规模的扩大,建设高质量教育评价体系尤为重要,中共中央和国务院印发的《深化新时代教育评价改革总体方案》(以下简称《方案》)中指出教育评价事关教育发展方向,有什么样的评价指挥棒,就有什么样的办学导向[3]。但目前仍没有系统的、完整的教学评价体系,我们从学习投入的角度出发,探索出了混合式教学评价指标和混合式教学评价标准,为建设高质量的教育评价体系提供思路;形成了学习预警模型,改变了传统的“事后处理”,建立了“事前、事中预防”的学习预警机制。
1 相关研究综述
1.1 学习预警研究
近年来,学习预警是教育数据挖掘研究和应用一个热点领域,国外学习预警的研究与实践始于 20 世纪 90 年代初,通过对国内文献的研究,发现国内最早研究学习预警的是华金秋,其《台湾高校学习预警制度及其借鉴》文献发表于 2007 年。学习预警普遍采用的算法有回归分析、并通过准率、召回率与 F 值等,本文使用了召回率、F 值和 ROC 曲线来衡量学习预警模型的泛化能力。唐婧通过研究各类学习预警算法的研究发现,学习成绩的预测应包含量化和非量化两种因素,因此预测学生学期末是否及格时可以采用决策树算法,而预测学生的整体表现时则要使用神经网络算法[4]。本研究属于单一成绩的预测,所以也构建了决策树预警模型。国内外学者也不乏使用决策树算法进行学习预警。Ya-Han Hu 使用数据挖掘技术来构建预警系统,通过研究发现,以 AdaBoost 为补充的分类和回归树(CART)是评估学习成绩的最佳分类器[5];MISHRA T 等人发现随机森林算法比 J48 算法对性能的预测更准确[6];HUSEYIN 等采用决策树预测学生学业成绩和影响学生学业成功的重要因素,并构建了一个完整的数据挖掘系统[7]。王磊等人比较了多种算法的学业预警模型,发现随机森林算法召回率最高是 87%[8];王改花使用决策树算法预警,所有的预测准确概率介于 70.25%~95.10% 之间[9];崔仁桀用决策树 C4.5 算法构建学习成绩预警模型,决策树学习预警模型的预测性能为 83%[10]。
综上可见,国内外学者在预警算法上的研究颇多,但大都是直接对收集到的数据进行分类决策,且预警过程不涉及评价方式。本文从学习投入的角度出发,首先使用结构方程模型将收集到的多维指标进行降维,并在学习投入模型的基础上,建立学习成效模型与学习预警模型,体现了评价模型与预警模型的一体化、科学性和可信度。
1.2 学习投入研究
20 世纪 80 年代初期,美国学者们就开始了对“学习投入”的研究,学习投入(academic engagement)源于工作投入,SCHAUFELI 将工作投入的研究扩展到学生学习投入中,率先提出了学习投入的概念[11]。为了解学习投入的研究现状,本文分析了中国知网(CNKI)、万方和维普三方数据库。以“学习投入+学习投入度”为关键词进行精确检索,共检索出 3447 篇文献,其中中国知网 1250 篇,万方数据库 1154 篇,维普数据库 1043 篇。使用 cooc6 软件对文献进行文献合并、检验并删除缺失作者或摘要的文献、人工筛选出与主题不符的文献,最后对三个数据库的文献进行去重并整理,最终得到与主题相关度高的 1024 篇文献。使用 CiteSpace 工具绘制关键词共现图谱。关键词可以概括一篇文献的研究方向,一般来说,频率和中心度较高的关键词可以代表该领域某一时期的学术研究热点,绘制的关键词共现图谱可以体现学习投入研究领域的主要内容[12]。
图 1 是 2000—2020 年我国学习投入文献的关键词共现图,图中节点大小代表关键词出现频次的多少,节点越大越能代表该关键词为学习投入领域的研究热点。本文将根据关键词将学习投入研究主题分为六类,分别是学习投入研究的维度、学习投入度的测量方法、学习投入依托的环境支持、学习投入的研究对象、影响学生学习投入的因素以及学习投入所产生的影响的研究。对于学习投入度所包含的维度,目前普遍接受 Fredricks 划分的行为投入、认知投入、情感投入三个维度[13]。在学习投入度测量上,目前常采用的测量方法是问卷调查法,最常用的是美国全国大学生学习投入度调查问卷(NSSE)汉化后的 nsse-china 问卷、2002 年 SCHAUFELI 等人以大学生为样本,编制的学习投入量表(Utrecht Work Engagement Scale-Student,UWES-S)[14]、2005 年英国的以学生为主体的高等教育质量评估的量表英国大学生学习投入调查 (United Kingdom Engagement Survey,简称 UKES)量表[15]以及澳大利亚和新西兰的大洋洲大学生学习投入调查 (Australasia Survey of Student Engagement,简称 AUSSE)[16]。在环境支持方面,学习投入度研究依托的教学环境是课堂和在线学习,本文依托的教学环境是混合式教学课堂。学习投入度的研究对象主要有中学生和大学生。影响学生学习投入的因素的因素是多方面的,有学者将其归为两类:一是人口统计学变量(如个体的性别、种族、家庭收入等)和个体特征变量(如倦怠、专业承诺、学习动机、学业情绪、自我效能感都等);二是环境变量,包括家庭(父母教养方式等)和学校(师生关系、同学关系等)等变量[11,17]。学习投入所产生的影响也是研究的热点,学习投入与学生的学习表现、学习成绩等因素有关,学习投入可以用来预测学生学习成绩。

本文将降维后的二维数据分别解释为认知投入和行为投入。认知投入指可能影响自身发展和心理求知需求的行为,与学习绩效相关,换言之是学习者利用认知策略调节自我学习的行为[18],认知投入可以表现在学生的学业成绩、知识掌握情况、学以致用情况等方面。行为投入指学生进行的机械的、形式的努力、专注与坚持的学习行为,它是情感投入和认知投入的载体,可以用来预测学习成就、学习成绩等情况[19]。本研究基于学习投入中的认知投入、行为投入对学生的混合式学习数据进行分析,利用认知投入和行为投入进行学习预警,从而构建学习预警模型。通过阅读文献发现,目前通过认知投入和行为投入进行学习预警的文献比较少,本文的研究以便抛砖引玉,为后期研究提供一些参考。
1.3 学习预警在混合式教学中的应用
学习投入是影响学生成绩的关键因素,如何在混合式教学中提高学生学习投入水平值得深入探讨。混合式教学是一个比较成熟的研究领域,VOCI E 和 YOUNG K 最早明确提出了混合式教学理念,为混合式教学的研究开创新猷。混合式教学的定义繁多,目前普遍接受的是:混合式教学是面对面教学与技术支持教学的结合[20]。混合式教学将传统的教学方式与在线学习的优势结合,既可以发挥教师的主导作用,又可以发挥学生的主体作用[21],形成了“主导主体相结合”的混合式教学模式。混合式教学的理论基础是建构主义理论,何克抗老师提出我们所倡导的建构主义不是那种建立在主观主义认识论和片面地以学生为中心教育思想基础上的极端建构主义,而是建立在 “主客观统一”认识论和 “主导—主体相结合”教育思想基础上的科学建构主义[22]。
我国对混合式教学的研究文献有很多,但是从学习投入的视角研究混合式教学,从而提高学习者学习投入水平,改进混合式教学方式等方面的文献较少,最早研究的 2016 年张艳红等人通过调研学生学习投入中存在的问题,分析混合式教学模式,为本科教学提出改进建议。研究混合式教学下的学习投入,可以帮助教师和管理者了解学习者在混合式教学中的学习行为,更好的评价教与学的质量,促进混合式教学评价体系的构建。
不少研究者发现,学习投入与学习成绩、学习效果等存在正向关系。表明学习投入是一个多维结构,可以用来预测学生学习成绩[23,24]。学习者学习投入度越高越有利于他们的学术进步和学业成就[25]。PISA2009 也将学习投入作为反映学生素养的重要指标之一,并以此来衡量教育质量[26],越来越多学者的观点认为学生学习投入度可以用来预测学生的学习质量。因此,我们可以从学生学习投入度的角度衡量、预测学生学习成绩。使用学习投入度对学生进行学习预警,国内外也有初步的研究,比如 Rahal 等人探索验证了教育心理学的动机成就理论与预测分析在初级定量商务课程中有助于提高学生学习成绩[27]。李爽从学习投入中的行为投入角度出发,结合在线案例课程数据对在线学习行为投入测量指标进行了分析,结果显示,四个学习行为投入指标对课程成绩有显著预测作用,能够预测成绩 26.9% 的变异[18]。王红梅等人发现行为投入、认知投入与期末成绩存在显著正相关的线性关系,可以用来预测学业成绩[28]。
2 研究基础
2.1 研究对象与数据来源
本研究以 S 市高校 2019 级和 2020 级参加大学物理课程的大学生为研究对象,共来自四个不同班级不同学期的混合式教学数据,分别是 2019 年春季学期采集的 Z 教师班级数据,共 143 名学生的混合式学习数据;2020 年春季学期采集的Z教师班级数据,共 84 名学生的混合式学习数据;2020 年春季学期采集的 S 教师班级数据,共 121 名学生的混合式学习数据;2020 年 2 月—2020 年春季学期采集的 W 教师班级数据,共 65 名学生的混合式学习数据。其中 Z 教师班级数据包括课堂应答系统数据、SPOC 平台数据和线下教学数据;S 教师和 W 教师数据包括 SPOC 平台数据和线下教学数据。
2.2 研究方法
1) 主成分分析
主成分分析(principal component analysis,PCA)是机器学习中常用的降维统计方法,它可以将多维相关变量降维成低维的不相关的综合变量,通常把转化生成的综合指标称为主成分,每个主成分尽可能地反映原始数据所提供的信息[29],为了方便后期应用集成,这里使用 Java 编写的主成分分析,具体步骤如下:
第一步计算 KMO 系数,KMO 可以进行相关性检验 只有相关性充分,才符合降低维数的要求,KMO>0.6 说明适合进行主成分分析;
第二步为消除量纲的影响,需要将原始数据标准化,使用的是 z-score 标准化;
第三步是建立各指标相关系数矩阵,使用的是 person 相关系数;
第四步是根据第三步的相关系数计算特征值和累计方差贡献率,根据特征值求出主成分;使用特征值大于 1 或者累计贡献值达到一定程度(一定程度指的是 50%[30])的方法来确定主成分的个数,本文根据特征值大于 1 的方法来确定主成分。
2) 验证性因子分析
本文使用 Amos 24.0 软件进行验证性因素分析(confirmatory factor analysis;简称CFA),因为认知投入与行为投入具有相关性,所以使用多因素斜交模型构建结构方程模型。使用主成分分析探索出最佳的因素结构,然后使用 CFA 验证因素结构模型以及指标变量是否可以有效作为因素构念(潜在变量)的测量变量[31]。
3) 聚类分析
本文使用的聚类分析工具为 SPSS Statistics26,SPSS Statistics 是 IBM 旗下的统计分析工具。聚类试图将数据集中的样本划分为若干个通常是不相交的子集,在数据挖掘中聚类算法可以分为划分方法、层次方法、基于密度的方法、基于网格的方法和基于模型的方法[32]。其中划分方法是聚类分析最简单、快速的方法之一,K-Means(K-均值)算法是划分方法的基本算法。使用 SPSS Statistics26 的 K-means 聚类算法对行为投入和认知投入数据进行聚类分析,K-means 聚类在使用前需要选择聚类的个数,我们选择聚类个数为 2,根据聚类结果中的聚类中心确定及格情况并进行编码。
4) 支持向量机
本文使用了 SPSS Modeler18.0 进行分析,SPSS Modeler 具有专业性、易用性、扩展性与高性能的特点。支持向量机(SVM)是针对二分类任务设计的,本研究中的二分类任务是学生及格情况,在 SPSS Modeler18.0 中其输入变量是表示行为投入度和认知投入度的连续数据,目标变量表示及格情况的离散数据(1 代表及格,0 代表不及格)。
5) 决策树
决策树是一种树型预测模型,是预测分类的常用方法,决策树方法的计算量比较小、可以处理连续和离散数据、能够生成易于理解的分类模型。常用的决策树算法有以信息增益为度量的 ID3 算法,以信息增益比为度量的 C4.5 算法,以 Gini 系数为度量的 CART 算法。C5.0 是在 C4.5 基础上改进的算法,包括了 C4.5 的全部功能[33],是 C4.5 的商业化版本,可以用来处理大数据。
本研究采用 IBM SPSS Modeler 18.0 软件构建学习预警模型,输入变量是表示行为投入度和认知投入度的连续数据,目标变量表示及格情况的离散数据(1 代表及格,0 代表不及格)。
2.3 探究混合式教学评价指标
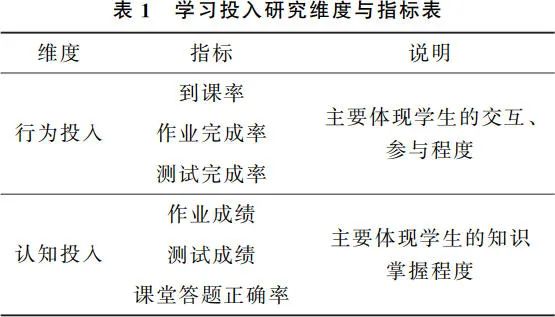
大量的研究为本文提供了如何选取测量指标的参考,依据收集的混合式学习数据并结合前人对学习投入维度的划分[23,34,35],本文从行为投入、认知投入两大维度开展研究,共使用以下六个指标来表征混合式教学评价指标(表 1)。
2.4 确定评估模型标准
精确度(precision,也叫查准率)和召回率(recall,也叫查全率)是评估模型性能的指标。其中精确度关注的是预测结果中错报的案例;查全率关注的是预测结果中漏报的案例。对于学习预警而言,漏报相比于错报更加严重,即将实际不及格的人预测为及格的情况更因该引起我们的重视,所以我们在评估模型的时候使用了召回率。
研究者们也常用查准率和查全率的调和平均值来比较模型优劣,即综合评价 F 值,公式如(1)。使用F 值作为评估学习预警性能的评价指标,能够同时考虑精准率和召回率。
其中,P 代表精确度,R 代表召回率。在本文中,P =(模型捕获的不及格人数)/(模型捕获的不及格人数+被模型误判的及格人数);R =(模型捕获的不及格人数)/(模型捕获的不及格人数+被模型误判的不及格人数)。
ROC(Receiver Operating Characteristic)全称是“受试者工作特征”曲线,ROC 曲线综合考虑了模型在不同任务下的“期望泛化性能”的好坏,通过比较 ROC 曲线下的面积即 AUC(Area Under ROC Curve)值的大小来评定模型孰优孰劣。本文同时将召回率、综合评价指标 F 值和 ROC 曲线作为模型性能度量的标准。
3 学习预警模型构建
3.1 确定认知投入、行为投入维度指标
为了研究行为投入、认知投入与混合式教学评价指标的关系,研究首先采用主成分分析对学习投入度指标进行探索性分析,然后通过构建结构方程模型进行验证。四个班级认知投入、行为投入维度的主成分分析结果如表 2 所示,由表可知主成分分析的 KMO 均在 0.6 以上,表明适合进行主成分分析,累积方差贡献率在 59.195%~72.294%,主成分可以反映原始数据信息。

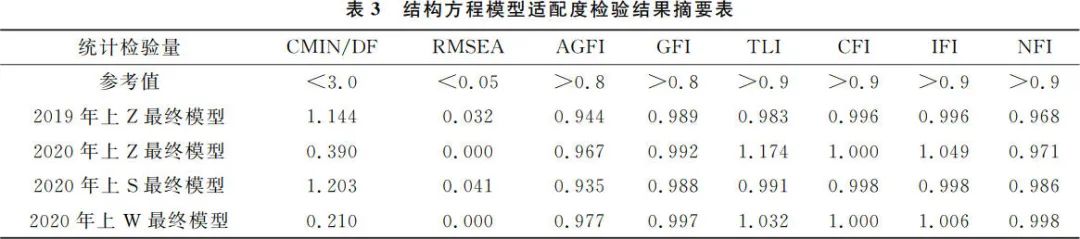
主成分分析后使用 Amos 24.0 对假设模型进行验证分析,通过对模型进行修正,最终拟合模型的整体模型适配度检验统计量值如表 3 所示,拟合结果显示,模型适配度指标都达到了适配标准,适配效果良好,说明使用主成分分析探索出的模型与实际观察数据的拟合效果良好,可以支持主成分分析探索出的模型。
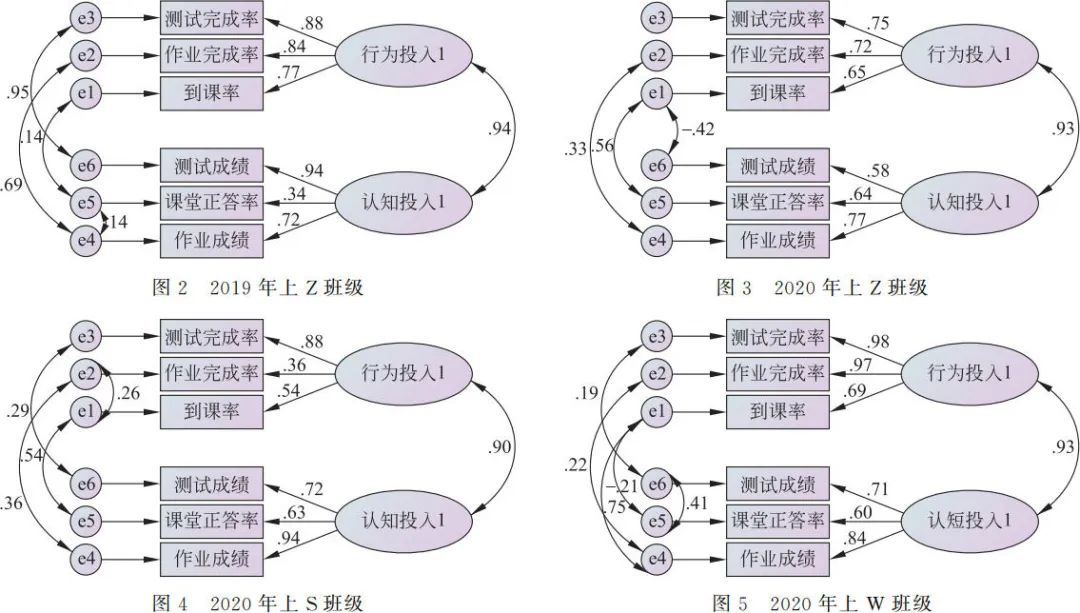
如图 2~图 5 是四个班级的标准化估计值模型,由模型可知因子载荷系数大都在 0.5~0.95,说明拟合效果良好。所以最终确定认知投入维度包含作业成绩、测试成绩、课堂答题正确率三个指标;行为投入维度包含到课率、作业完成率、测试完成率三个指标。
3.2 确定混合式教学评价标准
学习投入是学习主体学习过程的重要观测指标之一,也是学业成就的预测指标之一。认知投入作为学习投入中的深层次学习阶段,一直是教育学、认知心理学等领域的热点研究问题[36]。所以本文将认知投入作为过程评价,将期末成绩作为结果评价,通过过程评价与结果评价的占比来确定总评成绩,根据总评成绩进行学习预警。合理设定过程评价与结果评价的比重是确定混合式教学评价标准的关键,是保证学习预警有效性、科学性的关键。
为了确定总评成绩中过程评价与结果评价的比例,我们根据认知投入计算学生的总评成绩。主成分分析的成分矩阵如表 4 所示,表中系数为对应指标和认知投入的相关系数。根据成分矩阵我们可以得出期末成绩在教学评价标准中所占的权重,权重的计算公式如公式(2),其中 Wi 为因子的相关系数,αi 为因子的权重系数。那么我们可以得出 2019 年上 Z 班中期末成绩占比为 25.21%。
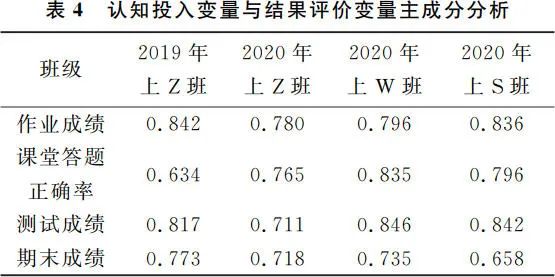
同理,根据公式 2 可以得出 2020 年上 Z 班中期末成绩占比为 24.11%;W 班为 22.88%;S 班为 21%,其均值为 23.3%,最终取期末成绩占比 23%,总评成绩计算公式表示为总评成绩=0.23×期末成绩+0.77×平时成绩。根据总评成绩判断学生是否通过,规定总评成绩大于等于 60 分为及格(编码为 1),总评成绩小于 60 分为不及格(编码为 0)。
这一结果与我们以往的评价方式有所不同,以往的评价方式是结果评价所占比例较高,但研究表明过程评价有助于提升教育供给质量,提高日常教学、服务、管理质量,故宜增加过程评价占比[37]。斯塔弗尔比姆(Stufflebeam)等人的 CIPP 的核心理念,也指出不能只重视结果评价,同时也要关注过程评价[38]。《方案》中也指出过程评价应居于四种评价中的核心地位,强化过程评价就是要扭转传统教育评价中只重结果评价的倾向[3]。在综合评价中合理设定过程评价与结果评价的比例,有助于提高教育评价的科学性、客观性和专业性。
3.3 多种预警模型比较
确定了评价标准与认知投入维度指标、行为投入维度指标后,将四个班级的数据进行合并共得到 413 名学生的混合式学习数据。
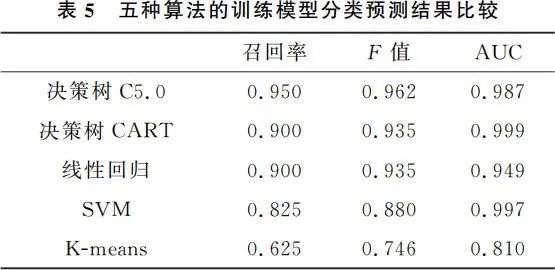
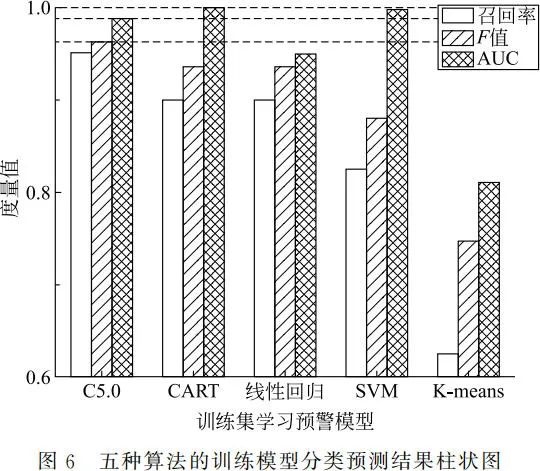
我们分别使用了决策树 C5.0、线性回归、决策树 CART、支持向量机和 K-means 聚类算法分别构建学习预警模型,表 5 是五种算法的训练模型分类预测结果比较,图 6 为五种算法的训练模型分类预测结果图。我们首要比较模型的 F 值,其次比较召回率和 AUC 值,从表 5、图 6 中可以看出决策树 C5.0 的性能最优;决策树 CART 与线性回归模型的召回率和 F 值性能相同且位居第二,但 AUC 值高于决策树 C5.0。
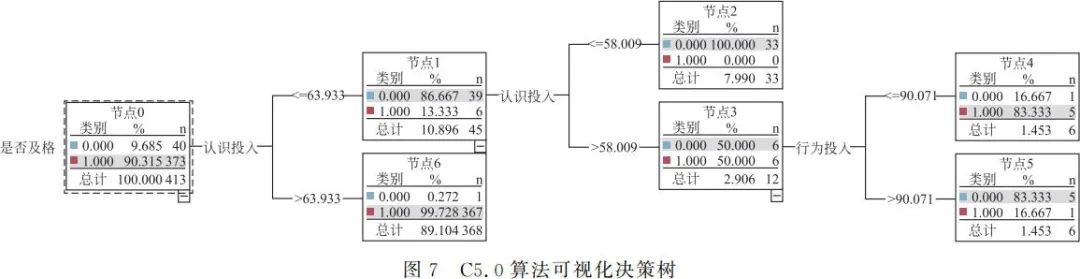
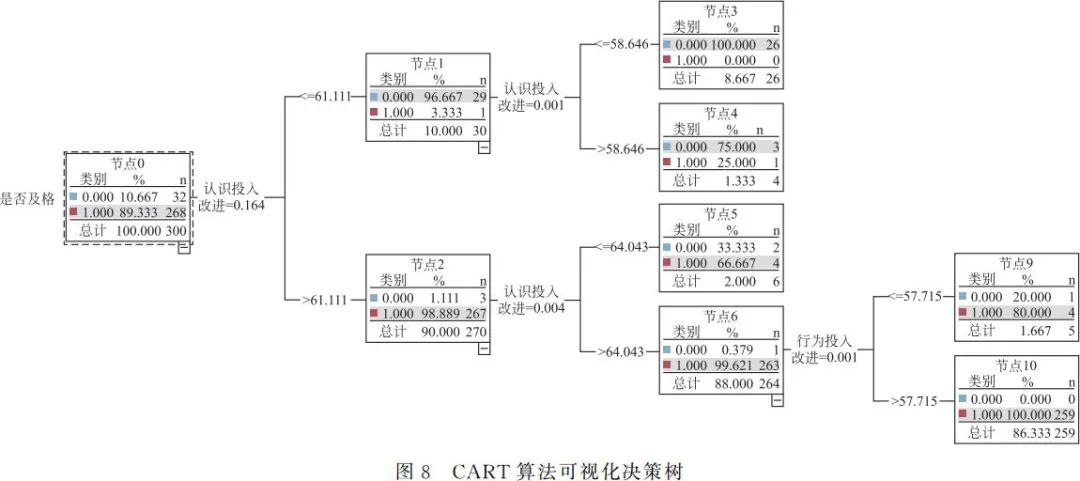
使用 SPSS modeler 构建学习预警模型时会生成可视化决策树模型,如图 7、图 8 所示是决策树 C5.0 和决策树 CART 生成的决策树模型,节点中 0 代表不及格,1 代表及格,不及格是风险人群。
3.4 预警模型测试
为了确定出最优学习预警模型,接下来使用测试集进行测试,测试使用决策树 C5.0 预警模型、决策树 CART 预警模型和线性回归预警模型,分别对测试集数据进行预测,通过比较预测结果的召回率、F 值和 ROC 曲线的 AUC 值来评估训练集模型性能,以确定最终的学习预警模型,为后期的应用集成奠定基础。
测试集验证了研究结果的科学性与可信度,使用收集到的 2020 年秋季学期收集的 H 教师班级数据作为测试集,共 112 名学生的混合式学习数据。利用已经生成好的决策树 C5.0 学习预警模型、决策树 CART 学习预警模型和线性回归学习预警模型,分别对测试集数据进行预测,最终测试集分类预测结果如表 6 所示。
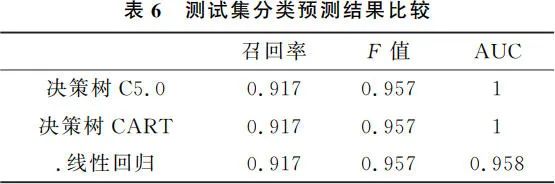
三个学习预警模型的召回率、F 值均相同,为了进一步确定最优学习预警模型,随后绘制了 ROC 曲线,图 9~图 11 展现的是 ROC 曲线结果,从图中可以明显看出决策树 C5.0 与决策树 CART 的 ROC 曲线相同。
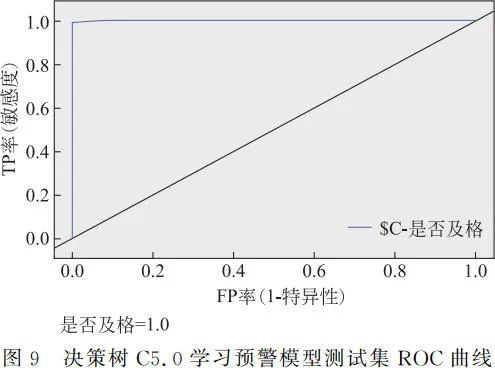
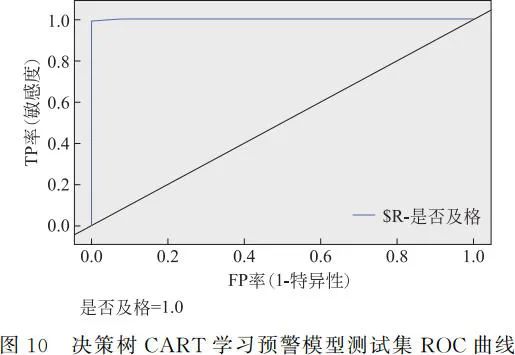
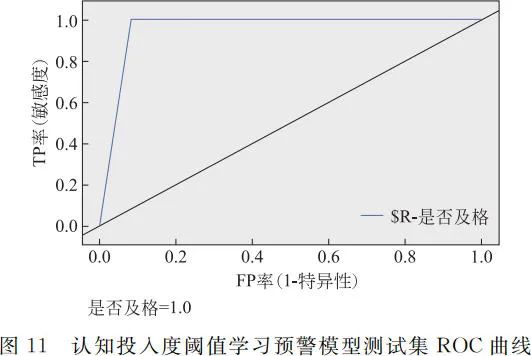
由以上训练集与测试集的结果,可以得出在本应用中决策树 C5.0 的性能与决策树 CART 的性能相同,且都超过 0.9,均可用于混合教学的预警模型。
4 结语
本文依托教育大数据技术从学习投入的视角出发,收集、过滤、融合、分析处理了混合式教学数据,从混合式教学数据中挖掘出混合式教学评价体系中的评价标准和评价指标,形成了混合式教学评价体系,为高质量教育评价提供参考。使用认知投入、行为投入对学生的学习成绩进行学习预警,通过训练及测试多种学习预警模型并比较学习预警模型的性能,最终选择决策树 C5.0 构建的学习预警模型。学习预警使教学实现了从“事后处理”到“事前、事中防御”的过渡,帮助决策者对教学进行科学指导,有效提升教学管理水平;帮助教师改进教学策略,提高教学水平、教学质量;帮助学生在平时学习中注重保持较高的学习投入度,避免出现考试时临时抱佛脚的情况,提高学生的学习质量。
目前,本文的研究尚处于半人工半智能化的状态,后期将会把主成分分析、决策树分类模型集成到智能学习管理系统中,完成学习预警模块的开发。形成数据采集、处理、挖掘、可视化科学分析、可自动预警功能于一体的学习预警系统。另外已有学者研究发现学习投入是一个动态的复合变量,其在学期的不同阶段,学生的学习投入会有差异,本文只研究了学生学期末的学习投入,构建学习预警模型,并使用学期末的数据进行测试。从笔者的研究结果来看,学习预警信号在学习中期即可展现稳定的学习预警效果。后期将会研究学生在一个学期不同学习阶段的学习投入,并通过实证研究验证预警模型的准确性与稳定性。
参考文献
[1]光明日报. “十四五”: 高等教育立足当下 更将引领未来[EB/OL]. http://www.moe.gov.cn/jyb_xwfb/s5147/202011/t20201123_501229.html, 2020-11-22.
[2]教育部. 中国教育概况——2019年全国教育事业发展情况[EB/OL]. http://www.moe.gov.cn/jyb_sjzl/s5990/202008/t20200831_483697.html, 2020-08-31.
[3]新华社. 中共中央 国务院印发《深化新时代教育评价改革总体方案》[EB/OL]. http://www.gov.cn/zhengce/2020-10/13/content_5551032.htm, 2020-10-13.
[4]唐婧. 数据挖掘算法在计算机教学成绩预测中的应用[J]. 信息与电脑(理论版), 2017(18): 34-36.
TANG J. The application of data mining algorithm in computer teaching prediction[J]. Information and computer (theoretical Edition), 2017(18): 34-36. (in Chinese)
[5]HU Y H, LO C L, SHIH S P. Developing early warning systems to predict students' online learning performance[J]. Computers in Human Behavior 36, 469-478. doi: 10. 1016/ j. chb. 2014. 04. 002.
[6]MISHRA T, KUMAR D, GUPTA S. Mining Students' Data for Prediction Performance[C]. Proceedings of the 2014 Fourth International Conference on Advanced Computing & Communication Technologies. IEEE, 2014.
[7]GURULER H, ISTANBULLU A. Modeling Student Performance in Higher Education Using Data Mining[M]. Berlin: Springer International Publishing, 2014.
[8]王磊, 赵芳芳. 高等职业院校分类招考背景下的学生学业早期预警研究[J]. 中国职业技术教育, 2017(32): 70-74.
WANG L, ZHAO F F. Research on students' academic early warning under the background of classified recruitment of Higher Vocational Colleges[J]. China Vocational and technical education, 2017(32): 70-74. (in Chinese)
[9]王改花, 傅钢善. 网络学习行为与成绩的预测及学习干预模型的设计[J]. 中国远程教育, 2019, No. 529(2): 43-52.
WANG G H, FU G S. Prediction of E-learning behavior and achievement and design of learning intervention model[J]. China distance education, 2019, No. 529(2): 43-52. (in Chinese)
[10]崔仁桀. 数据挖掘在学生专业成绩预测上的应用[J]. 软件, 2016, 37(1): 24-27.
CUI R J. Application of data mining in students' professional achievement prediction[J]. Software, 2016, 37(1): 24-27. (in Chinese)
[11]倪士光, 伍新春. 学习投入: 概念、测量与相关变量[J]. 心理研究, 2011, 4(01): 81-87.
NI S G, WU X C. Learning engagement: The conception, measurement and relevant variables[J]. Psychological research, 2011, 4(1): 81-87. (in Chinese)
[12]孙科, 李晓茜. 基于 Citespace 的大学生学习投入研究可视化分析[J]. 高等农业教育, 2019(4): 33-39.
SUN K, LI X X. Visualization analysis of College Students' learning input based on CiteSpace[J]. Higher agricultural education, 2019(4): 33-39. (in Chinese)
[13]FREDRICKS J A, BLUMENFELD P C, PARIS A H. School engagement: Potential of the concept, state of the evidence[J]. Review of Educational Research, 2004, 74(1): 59-109.
[14]张娜. 国内外学习投入及其学校影响因素研究综述[J]. 心理研究, 2012, 5(2): 83-92.
ZHANG N. Academic engagement:concepts, measurement, and factors[J]. Psychological research, 2012, 5(2): 83-92. (in Chinese)
[15]BOKHOVE C, MUIJS D. Can we reliably compare student engagement between universities? Evidence from the United Kingdom Engagement Survey[J]. Oxford Review of Education, 2019, 45(3): 417-434.
[16]COATES H. Development of the Australasian survey of student engagement (AUSSE)[J]. Higher Education, 2010, 60(1): 1-17.
[17]袁梦. 学生学习投入的影响因素及提升路径[J]. 教学与管理, 2020(15): 72-74.
YUAN M. Influencing factors and promotion path of students' learning investment[J]. Teaching and management, 2020(15): 72-74. (in Chinese)
[18]李爽, 王增贤, 喻忱, 等. 在线学习行为投入分析框架与测量指标研究——基于 LMS 数据的学习分析[J]. 开放教育研究, 2016, 22(2): 77-88.
LI S, WANG Z X, YU C, et al. Mining LMS data for behavior engagement indicators in online learning[J]. Open education research, 2016, 22(2): 77-88. (in Chinese)
[19]武法提, 张琪. 学习行为投入: 定义、分析框架与理论模型[J]. 中国电化教育, 2018(1): 35-41.
WU F T, ZHANG Q. Learning behavior engagement: Definition, analytical framework and theoretical model[J]. China audio visual education, 2018(1): 35-41. (in Chinese)
[20]马婧, 韩锡斌, 程建钢. 促进学习投入的混合教学活动设计研究[J]. 清华大学教育研究, 2018, 39(3): 67-75+92.
MA J, HAN X B, CHENG J G. Research on the design of mixed teaching activities to promote learning investment[J]. Educational research of Tsinghua University, 2018, 39(3): 67-75+92. (in Chinese)
[21]余胜泉, 路秋丽, 陈声健. 网络环境下的混合式教学——一种新的教学模式[J]. 中国大学教学, 2005(10): 50-56.
YU S Q, LU Q L, CHEN S J. Hybrid Teaching under the network environment—A new teaching model[J]. China University teaching, 2005(10): 50-56. (in Chinese)
[22]何克抗. 从 Blending Learning 看教育技术理论的新发展[J]. 国家教育行政学院学报, 2005(9): 37-48+79.
HE K K. New development of educational technology theory from blending learning[J]. Journal of National Institute of educational administration, 2005(9): 37-48+79. (in Chinese)
[23]APPLETON J J, CHRISTENSON S L, FURLONG M J. Student engagement with school: Critical conceptual and methodological issues of the construct[J]. Psychology in the Schools, 2010, 45(5): 369-386.
[24]ELLEN A, JENNIFER M S. Developmental Dynamics of Student Engagement, Coping, and Everyday Resilience[M]. New York: Springer US, 2012.
[25]FINN J D, ZIMMER K S. Student engagement: What is it? Why does it matter?[J]. Springer US, 2012.
[26]陆璟. PISA学习参与度评价[J]. 上海教育科研, 2009(12): 4-9.
LU J. PISA learning participation evaluation[J]. Shanghai Education and scientific research, 2009(12): 4-9. (in Chinese)
[27]RAHAL A, ZAINUBA M. Improving students' performance in quantitative courses: The case of academic motivation and predictive analytics[J]. International Journal of Management Education, 2016, 14(1): 8-17.
[28]王红梅, 张琪, 黄志南. 开放学习环境中学习行为投入与认知投入的实证研究[J]. 现代教育技术, 2019, 29(12): 48-54.
WANG H M, ZHANG Q, HUANG Z N. Empirical study of learning behavior engagement and cognitive engagement in open learning environment[J]. Modern educational technology, 2019, 29(12): 48-54. (in Chinese)
[29]周松林, 茆美琴, 苏建徽. 基于主成分分析与人工神经网络的风电功率预测[J]. 电网技术, 2011, 35(9): 128-132.
ZHOU S L, MAO M Q, SU J H. Wind power prediction of wind power based on principal component analysis and artificial neural network[J]. Power Grid Technology, 2011, 35(9): 128-132. (in Chinese)
[30]高桥信. 漫画统计学之因子分析[M]. 北京: 科学出版社, 2000.
[31]吴明隆. 结构方程模型[M]. 重庆: 重庆大学出版社, 2010.
[32]毕胜. 用 K 均值法对自考考生流失的研究[J]. 计算机时代, 2008(5): 48-51.
BI S. Study on the loss of self-taught candidates by K-means method[J]. Computer age, 2008(5): 48-51. (in Chinese)
[33]巩吉璋. 决策树分类算法在银行个人信用评级中的应用[D]. 暨南大学, 2008.
[34]周媛, 韩彦凤. 混合学习活动中学习者学习投入的研究[J]. 电化教育研究, 2018, 39(11): 99-105.
ZHOU Y, HAN Y F. Research on learners' learning engagement in blended-learningactivities[J]. Audio visual education research, 2018, 39(11): 99-105. (in Chinese)
[35]龚艺, 刘波, 谭明杰, 等. 远程教育中在线学习投入与学习绩效关系的实证研究[J]. 成人教育, 2018, 38(6): 24-28.
GONG Y, LIU B, TAN M J, et al. Empirical study of the relationship between online learning engagement and academic performance in distance education[J]. Adult education, 2018, 38(6): 24-28. (in Chinese)
[36]张晓峰, 李明喜, 俞建慧, 等. 面向学习云空间的认知投入量化研究[J]. 中国远程教育, 2020(5): 18-28+76-77.
ZHANG X F, LI M X, YU J H, et al. Quantifying cognitive engagement in cloud-based learning space[J]. China Distance Education, 2020(5): 18-28+76-77. (in Chinese)
[37]张志祯, 齐文鑫. 教育评价中的信息技术应用: 赋能、挑战与对策[J]. 中国远程教育, 2021(3): 1-11+76.
ZHANG Z Z, QI W X. Information technology in educational assessment: Empowerment, challenges and solutions[J]. China Distance Education, 2021(3): 1-11+76. (in Chinese)
[38]黄静宜. CIPP 课程评价模式简析[J]. 职业技术教育, 2005, 26(10): 38-39.
HUANG J Y. Comment of CIPP pattern of curriculum evaluation[J]. Vocational and Technical Education, 2005, 26(10): 38-39. (in Chinese)
基金项目: 2020年度上海市教育科研市级课题“大学物理交互式电子书设计与教学实践”项目(编号:C20122)
通讯作者: 张睿,同济大学副教授,主要从事教育技术与物理教育研究工作,zr2002_7@163.com。
引文格式: 李亚楠, 张睿. 基于学习投入的混合式教学预警模型研究——以大学物理为例[J]. 物理与工程, 2022, 32(1): 93-102, 125.
Cite this article: LI Y N, ZHANG R. Research on early warning model of hybrid teaching based on learning engagement—Taking college physics as an example[J]. Physics and Engineering, 2022, 32(1): 93-102, 125. (in Chinese)
END

更多精彩文章请点击下面“蓝字”标题查看:
对麦克斯韦方程组拓展的评论王青教授:深入理解“拓展的麦克斯韦方程组”——2.0版王青教授:理解王中林院士“拓展的麦克斯韦方程组”“碰瓷”麦克斯韦:伽利略协变和洛伦兹协变电磁场论趣谈热点:运动介质洛伦兹协变电磁理论2021年《物理与工程》优秀论文、优秀审稿专家、优秀青年学者名单王青教授:源自苏格拉底的问题驱动式教育——在互动中共同学习和成长读后感:教育中的现实和远方王青教授:昨晚(6月9日),清华电动力学期末考试朱邦芬院士:“减负”误区及我国科学教育面临的挑战《物理与工程》2021年第6期目录乐永康:新冠肺炎疫情防控下美国物理实验教学及中美情况对比顾牡:对于重新制定的《非物理类理工学科大学物理课程教学基本要求》的认识和体会朱邦芬院士:从基础科学班到清华学堂物理班朱邦芬院士:对培养一流拔尖创新人才的思考李学潜教授:物理是一种文化李学潜教授:如何帮助物理系学生迈过从高三到大一这个坎穆良柱:物理课程思政教育的核心是科学认知能力培养穆良柱:什么是物理及物理文化?穆良柱:什么是ETA物理认知模型穆良柱:什么是ETA物理教学法吴国祯教授:我的国外研究生经历印象——应清华大学物理系“基科班20年·学堂班10年纪念活动”而写
陈佳洱,赵凯华,王殖东:面向21世纪,急待重建我国的工科物理教育王亚愚教授:清华物理系本科人才培养理念与实践葛惟昆教授:关于中外人才培养的几点思考安宇教授:为什么传统的课堂讲授模式需要改变安宇教授:其实教学就是积累的过程刘玉鑫教授:关于本科生物理基础课程教学和教材编著的一些思考沈乾若:重创理科教育的美加课程改革Henderson C:美国研究基金支持下的物理教育研究及其对高等物理教育的影响《物理与工程》期刊是专注于物理教育教学研究的学术期刊,是中国科技核心期刊,1981年创刊,欢迎踊跃投稿,期刊投审稿采编平台:
http://gkwl.cbpt.cnki.net
欢迎关注
《物理与工程》微信公众号
原标题:《基于学习投入的混合式教学预警模型研究——以大学物理为例》
