原创 刘朋帅 周晨 等 物理与工程

摘 要

空间磁感应强度的计算，对于基于电磁感应原理的电子产品的设计和仿真、电子产品的安全性能评估具有重要意义。本文主要研究空间曲线形式的线圈恒流条件下在各向同性空间任一位置磁感应强度的计算方法。本文通过毕奥-萨伐尔定律和叠加原理，应用向量叉乘的计算方法，推导出了空间曲线形式的线圈恒流条件下在各向同性空间任一位置磁感应强度，并给出了通用计算公式及公式的使用条件。应用本文所给出的通用公式，对典型平面线圈的空间磁感应强度公式进行了推导，计算了椭圆截面螺线管部分位置磁场强度的分布情况。本文得出的普遍公式计算简洁，对平面型和空间型线圈具有普遍的适用性。

关键词 空间曲线型线圈；磁感应强度；椭圆截面螺线管；普遍公式

Abstract The calculation of space magnetic induction is of great significance for design，simulation and the safety performance evaluation of electronic products based on the principle of electromagnetic induction. This paper studies the calculation method of magnetic induction intensity at any position in isotropic space under the condition of constant current of coil in the form of spatial curve.Based on Biot-Savart law and superposition theorem, this paper deduces the magnetic induction intensity at any position in isotropic space under the condition of constant current in the form of space curve by using the calculation method of vector cross product as well as giving the general calculation formula and the application conditions of the formula. Applying the general formula given in this paper, The space magnetic induction intensity formula of typical planar coil is deduced，and the magnetic field intensity distribution of the solenoid with elliptical cross section is calculated. It is concluded that the general formula is simple in calculation and is universally applicable to planar and spatial coils.

空间磁感应强度的计算，对于基于电磁感应原理的电子产品的设计和仿真、电子产品的安全性能评估具有重要意义。

在国内外的相关研究中，大部分是基于毕奥-萨伐尔定律和叠加原理，对平面曲线形式的线圈（如圆线圈、矩形线圈等）全空间磁感应强度求解，部分学者还研究了平面曲线形式的多匝线圈的全空间磁感应强度求解[1,2]；此外，有学者对空间特殊曲线形式的线圈（如长直密绕螺线管）全空间磁感应强度进行了研究[3]。但对于空间曲线形式线圈的全空间磁感应无统一的方法。本文将从毕奥-萨伐尔定律和叠加原理出发，研究空间曲线形式线圈的全空间磁感应强度计算的一般方法。

1 毕奥-萨伐尔定律

毕奥-萨伐尔定律由法国科学家毕奥和萨阀尔提出，是由实验得出的实验定律。它给出了磁场对场源电流的依赖关系，提供了研究电动力学的数学理论依据。此定律适用于载流导体电流呈稳定分布的情况[7]。

通过该定律可知，当闭合回路中有恒定的电流通过，可知在闭合回路外中某一点 P 处所产生电磁感应强度为[4]

上式中，r 为电流元到点 P 的矢量，dl 为电流元的矢量。P 点的总磁感应强度可以通过对载流导体产生的磁场积分得到[1]。

对于电流源 dl 产生的磁场强度dB，该定律也可表示为公式（2）的形式[1]

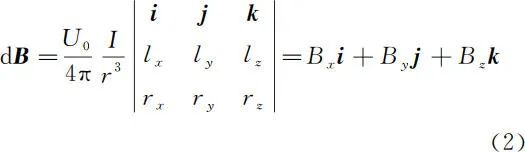
2 空间曲线型线圈全空间磁感应强度一般公式

假设电流元所在线圈为空间曲线形式，且该空间曲线 S 可导，则 S 可以表达为如下所示参数方程

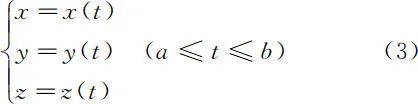
对 S 求导，得

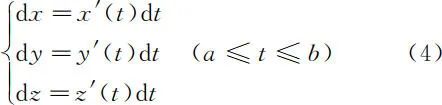
在各向同性空间，电流元矢量 dl 可表达为下列形式

假设 P 点坐标为（x 0，y 0，z 0），电流元到点 P 的矢量 r

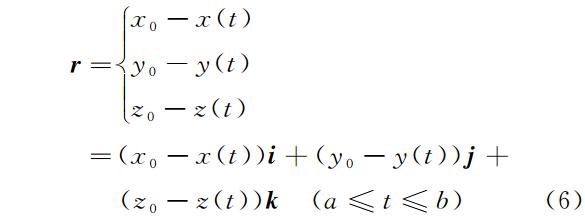
电流元在 P 点产生的磁场

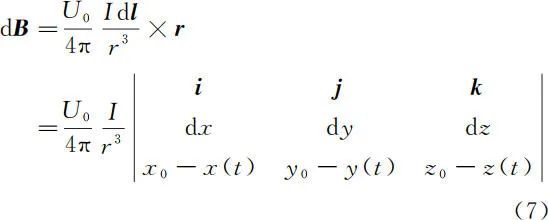
所以 P 点的磁感应强度为

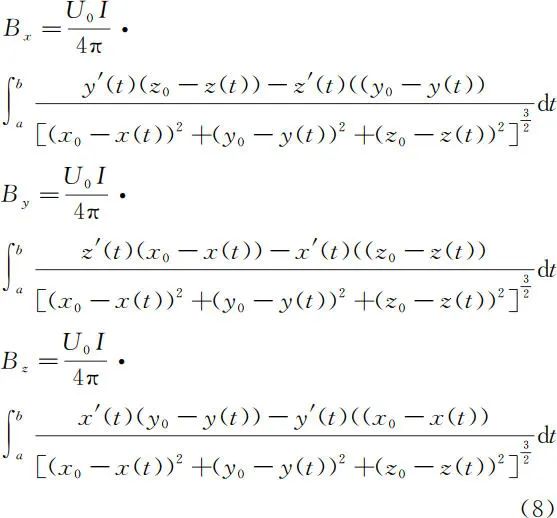
由上述推导和叠加原理，可得出如下结论：

对于空间曲线型线圈，其模型可用空间曲线表达，且该曲线满足如下要求：

(1) 该曲线可以分割为有限个子区间；

(2) 在分割的任一子区间内可导。

则该空间曲线所对应的线圈在恒定电流通过的条件下，可依据毕奥-萨伐尔定律和叠加原理，求出该空间曲线形式的线圈在空间任一位置所激发的磁场强度。

3 应用

3.1 典型平面线圈磁场强度推导

平面线圈是空间曲线型线圈的特殊情况（Z = 0），本文所提出的空间曲线型典型平面线圈全空间磁感应强度公式，同样适用于平面线圈。典型的平面线圈，如通电直导线（包括有限长和无线长）、圆线圈等，在空间特殊位置的计算公式已经非常成熟。通常情况下[8],在公式推导过程中，会进行坐标处理，从而方便计算；此外呢，求出的磁场公式应用的范围不全，主要集中在一些特殊的点和轴线。本节将采用文中提出的磁场强度计算方法，来典型的平面线圈的全空间磁场强度。

对于通电直导线（图 1），其参数方程为

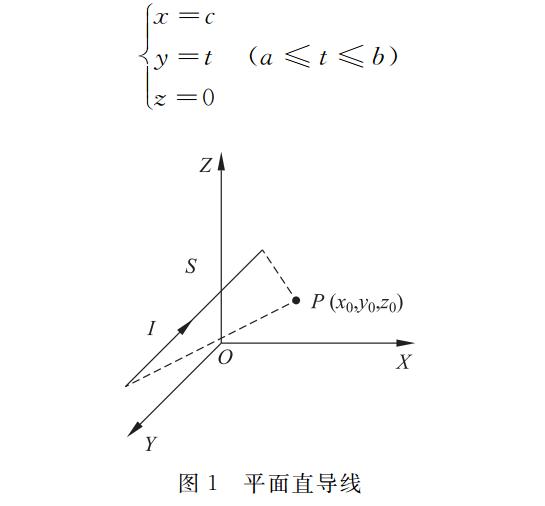
假设空间 P 点坐标为（x 0，y 0，z 0），将参数方程中的参数直接代入公式（8），得

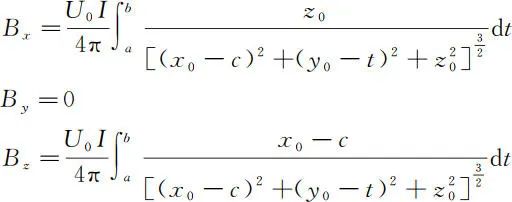
当通电直导线与 Y 轴重合，P 点位于 X 轴上时，既 c = 0，P 点坐标为（x 0，0，0）（x 0 ≠ 0）结果可简化为

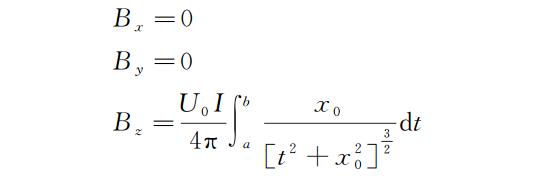
该结果与公认的通电直导线周围磁感应强度大小的公式（9）等价

对于通电圆线圈，其参数方程为

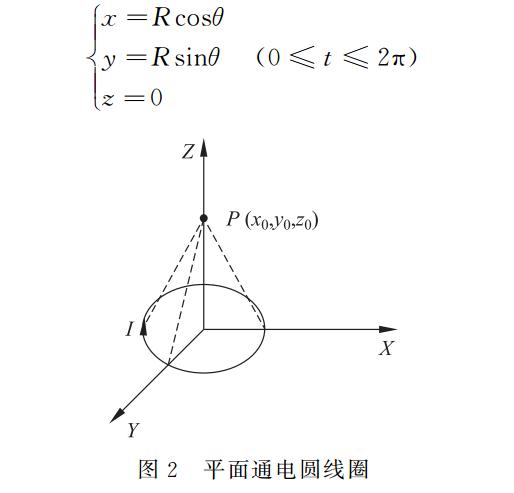
假设空间 P 点坐标为（x 0，y 0，z 0），将参数方程中的参数直接代入公式（8），得

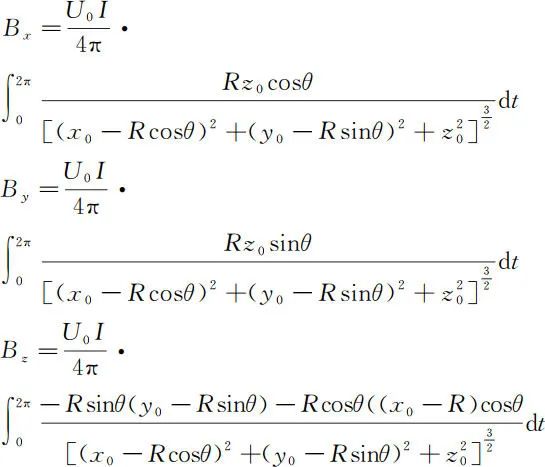
当 P 点位于 Z 轴上时，既 P 点坐标为（0，0，z 0）结果可简化为

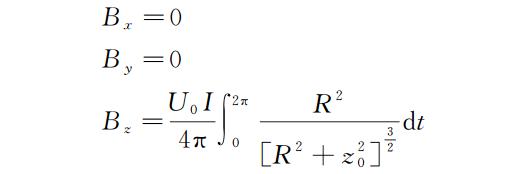
该结果与公认的通电圆线圈轴线上任意一点强度大小的公式（10）等价

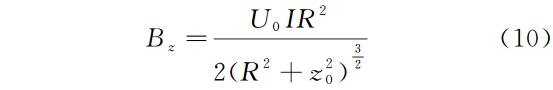
本节通过应用普遍公式对典型平面线圈磁场强度推导，并与公认的典型平面线圈的空间磁感应强度公式推导过程和结果进行比较，可得出以下结论：

(1) 本文所提出的普遍公式对于平面曲线线圈具有更加普遍的适用性；

(2) 推导过程简洁，无需对模型进行坐标处理；

(3) 推导结果与现有典型平面线圈磁场强度计算公式等价，现有典型平面线圈磁场强度计算公式是普遍公式在特殊物理数学场景下的特殊应用。

3.2 椭圆截面螺线管的磁场分布

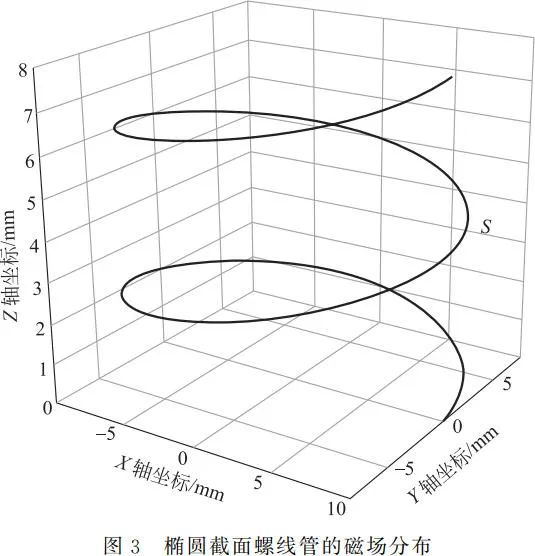
螺线管是用得最多的一种基本线圈形式, 应用于军事 、经济 、生态、医疗、天文、地质等众多领域中[5-6]。本节通过第 2 节方法计算椭圆截面螺线管的磁场分布，以验证本文所提出的方法的有效性和适用性。

如图 3 所示，椭圆截面螺线管的参数方程为

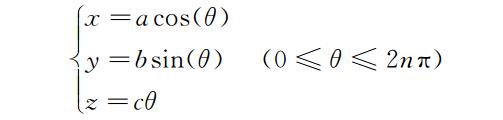
式中，n 为线圈匝数。

假设 P 点坐标为（x 0，y 0，z 0），将参数方程中的参数直接代入公式（8），得

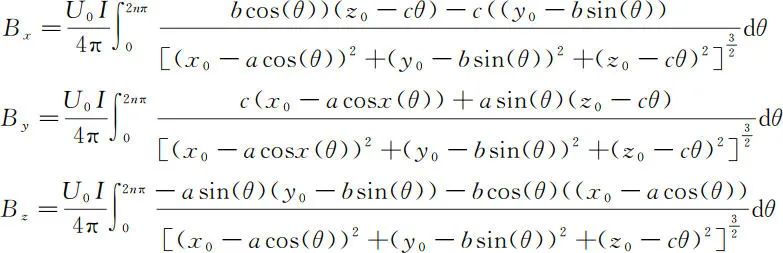
设椭圆螺线管的参数 a = 10mm，b = 8mm，c = 2/πmm，n =2。螺线管中通 1A 的电流，通过对 B z 进行积分运算，可得出该螺线管沿 Z 轴方向磁感应强度的大小，见图4。

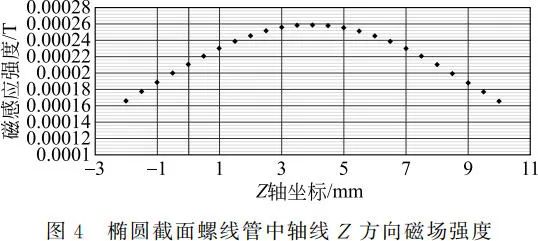
本节应用普遍公式对空间椭圆截面螺线管磁场强度进行计算，给出了空间椭圆截面螺线管的轴线和某一截面的 Z 方向磁场分布情况，表明普遍公式对于空间复杂曲线型线圈的磁场强度计算同样具有良好的适用性。

4 结语

本文通过毕奥-萨伐尔定律和叠加原理，应用向量叉乘的计算方法，推导出了空间曲线形式的线圈恒流条件下在空间任一位置磁感应强度，并给出了通用计算公式及公式的使用条件。应用本文所给出的通用公式，对典型平面线圈的空间磁感应强度公式进行了推导，计算了椭圆截面螺线管部分位置磁场强度的分布情况。得出了普遍公式具有计算简洁，对于平面型和空间型线圈具有普遍适用性的结论。

参考文献

[1]KONG L F, DU S X, LI Y W. Study on the distribution of the magnetic field of circular and square exiting coils in electromagnetic flow meter[J]. International Journal of Computer Science Issues, 2013, 10(2): 278-284.

[2]周敏, 田大庆, 李小润, 等. 多层圆线圈在电磁计算中全空间磁感应强度 B 的分布[J]. 制造业自动化, 2016, 38(3): 18, 19, 21.

ZHOU M, TIAN D Q, LI X R, et al. The full space distribution of magnetic induction intensity B of multi layer circular coils in electromagnetic calculation[J]. Manufacturing Automation, 2016, 38(3): 18, 19, 21. (in Chinese)

[3]张贵银, 贾彦枝. 载流长直密绕螺线管磁场的全空间解[J]. 现代物理知识, 2000(S1): 155.

ZHANG G Y, JIA Y Z.Full space solution of the magnetic field of a long current carrying solenoid[J]. Modern Physics Knowledge, 2000(S1): 155. (in Chinese)

[4]黎宇洲. 基于电磁感应技术的手机无线充电器设计与实现[D]. 成都: 成都理工大学, 2016.

[5]冯旺军, 魏智强, 秦晓静, 等. 密绕椭圆截面螺线管电流的磁场分布[J]. 兰州理工大学学报, 2006, 32(5): 158-160.

FENG W J, WEI Z Q, QIN X J, et al. Magnetic field distribution of the current in a tightly wound solenoid with elliptical cross section[J]. Journal of Lanzhou University of Technology, 2006, 32(5): 158-160. (in Chinese)

[6]MICHALSKI A, STARZYNSKI J, WINCENCIAK S. 3-D approach to designing the excitation coil of an electromagnetic flow meter[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(4): 833-839.

[7]孟祥国, 张宝锋, 崔风华, 等. 由麦克斯韦方程组推导出毕奥一萨伐尔定律的几种方法[J]. 聊城大学学报(自然科学版), 2004, 17(1): 25, 26, 65.

MENG X G, ZHANG B F, CUI F H, et al. Several methods of deriving Biot-Savart law from Maxwell equations[J]. Journal of Liaocheng University, 2004, 17(1): 25, 26, 65. (in Chinese)

[8]王建成, 陈燊年. 磁各向异性的毕奥一萨伐尔定律及其应用[J].华侨大学学报(自然科学版), 1989(10): 125-132.

WANG J C, CHEN S N. Biot-Savart law of magnetic anisotropy and its application[J]. Journal of Huaqiao University, 1989(10): 125-132. (in Chinese)

作者简介：刘朋帅，男，工程师，主要从事电子产品安全标准科研工作，研究方向为电磁技术在电子产品中的应用与安全，liups@cesi.cn；

周晨，男，工程师，主要从事电子产品安全标准科研工作，研究方向为电磁技术在电子产品中的应用与安全，zhouchen@cesi.cn。

引文格式: 刘朋帅, 周晨, 何鹏林, 等. 空间曲线型线圈在各向同性空间磁感应强度的分布[J]. 物理与工程, 2022, 32(1): 37-40,46.

Cite this article: LIU P S, ZHOU C, HE P L. The full space distribution of magnetic induction intensity of space curve coils in electromagnetic calculation[J]. Physics and Engineering, 2022, 32(1): 37-40,46. (in Chinese)

END

更多精彩文章请点击下面“蓝字”标题查看：

对麦克斯韦方程组拓展的评论王青教授：深入理解“拓展的麦克斯韦方程组”——2.0版王青教授：理解王中林院士“拓展的麦克斯韦方程组”“碰瓷”麦克斯韦：伽利略协变和洛伦兹协变电磁场论趣谈热点：运动介质洛伦兹协变电磁理论2021年《物理与工程》优秀论文、优秀审稿专家、优秀青年学者名单王青教授：源自苏格拉底的问题驱动式教育——在互动中共同学习和成长读后感：教育中的现实和远方王青教授：昨晚（6月9日），清华电动力学期末考试朱邦芬院士：“减负”误区及我国科学教育面临的挑战《物理与工程》2021年第6期目录乐永康：新冠肺炎疫情防控下美国物理实验教学及中美情况对比顾牡：对于重新制定的《非物理类理工学科大学物理课程教学基本要求》的认识和体会朱邦芬院士：从基础科学班到清华学堂物理班朱邦芬院士：对培养一流拔尖创新人才的思考李学潜教授：物理是一种文化李学潜教授：如何帮助物理系学生迈过从高三到大一这个坎穆良柱：物理课程思政教育的核心是科学认知能力培养穆良柱：什么是物理及物理文化？穆良柱：什么是ETA物理认知模型穆良柱：什么是ETA物理教学法吴国祯教授：我的国外研究生经历印象——应清华大学物理系“基科班20年·学堂班10年纪念活动”而写

陈佳洱，赵凯华，王殖东：面向21世纪，急待重建我国的工科物理教育王亚愚教授：清华物理系本科人才培养理念与实践葛惟昆教授：关于中外人才培养的几点思考安宇教授：为什么传统的课堂讲授模式需要改变安宇教授：其实教学就是积累的过程刘玉鑫教授：关于本科生物理基础课程教学和教材编著的一些思考沈乾若：重创理科教育的美加课程改革Henderson C：美国研究基金支持下的物理教育研究及其对高等物理教育的影响《物理与工程》期刊是专注于物理教育教学研究的学术期刊，是中国科技核心期刊，1981年创刊，欢迎踊跃投稿，期刊投审稿采编平台：

http://gkwl.cbpt.cnki.net

欢迎关注

《物理与工程》微信公众号

原标题：《空间曲线型线圈在各向同性空间磁感应强度的分布》