原创 冬青子 世界顶尖科学家论坛

阿喀琉斯在希腊神话中有“希腊第一勇士”之称,然而生活在公元前5世纪的古希腊哲学家芝诺(Zeno of Elea)却提出了一个悖论,表示这位勇士竟然跑不过一只乌龟。而这如同玩笑般的说法,只是芝诺的几个著名悖论之一。

追龟悖论示意图 图|WSJ
近日,2004年诺贝尔物理学奖获得者、世界顶尖科学家协会(WLA)会员弗兰克·维尔泽克(Frank Wilczek)在华尔街日报发表了专栏文章,探讨了由上述哲学家芝诺的悖论而引发了的数以千计需要解决的数学和物理问题。

弗兰克·维尔泽克 图 | ASU News
悖论展示了我们思维的缺陷
维尔泽克说,当对某种情况的不同思考方式导致了矛盾的结论时,悖论就产生了,而这些悖论中的矛盾现象在自然界里并没有出现,这暗示了我们在思维上尚存缺陷,它们更能激励我们在学术上走得更深远。

爱因斯坦 图|seattlechinesetimes
他认为,“悖论在物理学的历史上扮演了十分光荣的角色。”他举了个例子,阿尔伯特·爱因斯坦在16岁时就曾设想,如果自己能追上一束光,就能看到与现有物理定律相矛盾的事物;而经过十年的思考,爱因斯坦的狭义相对论证明了为什么光无法被追上。
诺贝尔文学奖获得者、英国哲学家伯特兰·罗素曾评论:“从芝诺时代至今,期间所建立的所有时间、空间与无限的理论,在某种形式上,都能在芝诺的悖论里找到依据。”

伯特兰·罗素 图|Tinting History
而维尔泽克进一步分析道,芝诺的悖论可以归结为三种:无限(infinity)悖论,零度(nullity)和悖论停滞(stasis)悖论。
三种悖论
关于无限悖论的具体说法,以“阿喀琉斯悖论”为例:
乌龟和阿喀琉斯赛跑,但乌龟的起点位于阿基里斯身前1000米处,且假定阿基里斯的速度是乌龟的10倍。
当比赛开始后,若阿喀琉斯跑了1000米,设所用的时间为t,此时乌龟便领先他100米;当阿喀琉斯跑完下一个100米时,他所用的时间为t/10,乌龟仍然领先他10米;当阿喀琉斯跑完下一个10米时,他所用的时间为t/100,乌龟仍然领先他1米,无限循环之后,乌龟始终领先阿喀琉斯一点点。由此,芝诺提出,阿喀琉斯可以无限逼近乌龟,但永远无法追上。
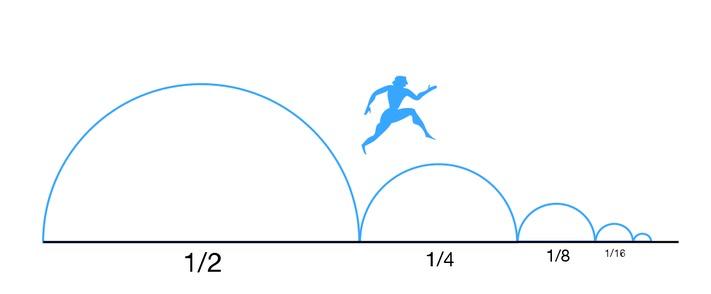
阿喀琉斯悖论 图|Forbes
而关于零度的悖论,也很有意思:通常认为,线是由无数个点构成的,但人们定义了“点”的长度是0,那为何无数个“0”加起来,就能成为一条有长度的“线”呢?
听上去更神奇的是停滞(stasis)的悖论,如“飞矢不动”,即一支飞行的箭是静止的——因为每一时刻这支箭都有其确定的位置,所以它是静止的,不能处于运动状态。然而,一只正在飞的箭怎么可能不在运动之中呢?
显而易见,这些悖论中的现象都与我们的常识极其不符——明明知道是错的,但从芝诺的说法出发,又似乎无从反驳。
这对于好奇心旺盛的学者们来说,如猫爪挠心;然而直到近代,学界才出现令人满意的解释。
芝诺悖论的一些解释
对于第一种无限悖论,在19世纪,数学家们诠释了应该如何处理递减项的无穷和。该理论表明,当这些和“收敛”时,会有一个定义明确的、有限(而不是无限的)答案。即阿喀琉斯能够在一个有限的时间内追上乌龟,而不是无限逼近。
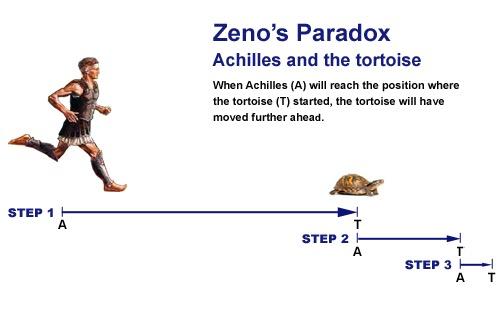
追龟悖论示意图 图|Publish0X
到了20世纪,对于第二种零和悖论,数学家们证实了这样一个事实:通过增加足够多次数的零,实际上结果可以超过零。这类问题在数学领域与微积分有关的高级章节“测度理论(measure theory)”中有讨论。“这一章节是出了名的狡猾和抽象。”维尔泽克评论道。
而对于第三种停滞悖论,如飞矢不动,则是在如今的物理学中,基于时空连续统一体理论(space-time continuum),得到了解释。这个理论来自于爱因斯坦的研究,即时间和空间并非相互独立且无关的现象,而是交织成一个跨越多个维度的连续体,时空。它的维度是四,即在三维空间坐标系中再加上一维的时间。而这样一来,在这个“四维坐标系”中,当把时间-空间作为离散点来处理时,飞行的箭可以在每个滴答的时间点,从一个位置跳到另一个位置,从而实现移动。维尔泽克举了个更为直观的例子来说明,即数字时代的电影,一部电影就是由一系列的画面快速播放形成的。
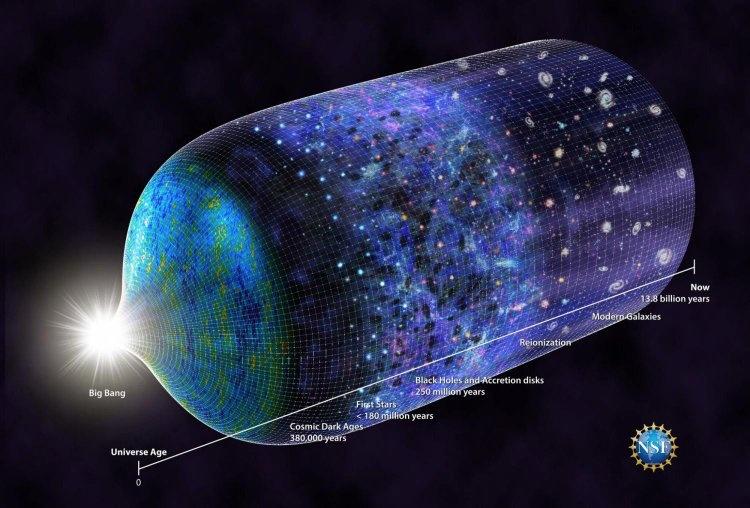
以时空连续体的形式来呈现宇宙大爆炸至今的过程
图|NSF
最后,维尔泽克也提出了一个悖论。牛顿曾说,大自然从来不会做徒劳无益的事情,它喜欢简单而非华而不实,“那么,为什么自然界没有把自己数字化,以避免类似芝诺的微妙悖论呢?”维尔泽克说道,“可以把这也看做一个悖论。芝诺仿佛依旧还活着。”
