危机不慌|走不出危机,因为知识陷阱
爱因斯坦说:我们按照理论找寻世界。他这么说,是为了强调知识体系对人类活动的巨大影响。我们观察到许多企业被同一块石头绊倒,很大程度上是因为落入了知识体系的陷阱。作为一种社会现象,危机与自然科学有很大差异。它是活跃的社会活动中的小概率事件。一方面,大数据分析和平均值知识不能通用;另一方面,厚数据也不能包打天下。危机管理需要有选择地运用四种知识体系。
在前面“长态危机社会”中,我解释过,一方面危机不断,另一方面,每个危机都有自身的特别属性,每次危机都需要视之为小概率事件。如果因为危机不断,就套用大数据分析的方法去找规律,我们极其容易陷入大数据分析的陷阱。
第一个陷阱是无差别套用数理统计正态分布的思维。一位共享车司机一年出车千次,从来没有遇过警察。疫情放松后去酒吧,以为自驾回家遇到警察的概率是千分之一。殊不知,没有喝酒的取样与有喝酒的取样是不能混杂统计的。这位兄弟至今还以为自己数学好,但运气差。
第二个陷阱是错把“同时出现”(Co-occurrence)当作因果关系。有人迷信自己喜欢的球队和股市涨跌的关系。美国超级碗杯橄榄球赛的一些球迷就犯过错误。从1967年第1届到1997年第31届,只要是NFL联赛出线队嬴,当年股市就大涨14%以上。如果是AFL联赛出线队嬴,股市就大跌10%。按这个统计规律买卖股票的球迷可能会输掉衬衫。1998年,丹佛野马队(AFL)嬴,当年股市大涨28%。2008年,纽约巨人队(NFL)嬴,股市不仅大跌35%,还落入次贷金融危机。
第三个陷阱是推导统计意义上的相关性为必然的因果关系。美国政府统计机构每年公布超过45000类的经济数据。如果你想研究失业率和利率之间关系受其他变量影响,你可以整理出成千上万个假设。有足够的大数据,找到相关性并不难。物理学家费米(Enrico Feimi)曾引述纽曼(John von Neumann)对数据可操纵性的生动表述:“给我四个变量,我可以搞出一头大象,再加一个,我还能让象鼻子扭动起来。”
第四个陷阱与危机事件的小概率特征有关。大数据分析推演出来的规律往往是“中值/平均值知识”。小概率事件一般出现在概率分布的变差中。例如,“六西格玛”质量控制的思维基于生产质量的正态分布和平均值。但是,对于过去没有发生过的危机事件,它的思维体系不仅无效,而且误导。
马克·吐温戏虐道:谎言、无耻的谎言、统计数据。我们也可以把它当成对大数据陷阱的警告。
所以,大数据分析比较适合大概率事件,有通用性质的规律,数量多的参数,以及即使境况改变也规律如旧的情况(见下图)。
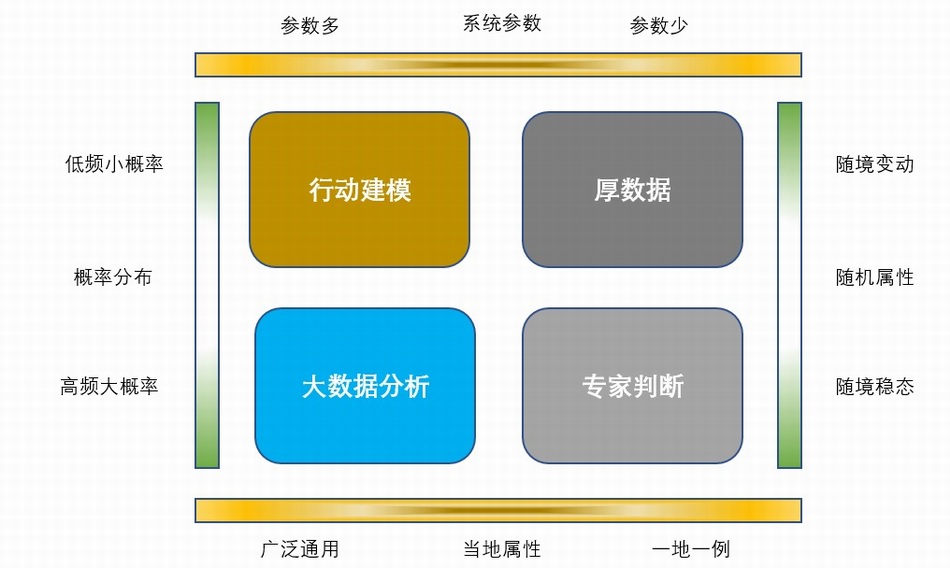
相比而言,危机事件发生概率低,并且受具体情境影响大。如果涉及到的参数变量少,我们要学会如何从小概率事件中获得对现象的深厚理解。例如,飞机制造商对每一次飞行事故都建立一个详细的档案,试图从小样本中建立对事故周全的理解。如果参数变量多,主事人就需要勇敢实践,用行动去影响和带动周围的利益相关者。例如,未来情境规划(Scenario planning)中的一条规律是主动、积极地与利益相关者沟通。你的洞见会影响其他人的思维,进而被认可为值得遵循的共同规律。
二战期间,德累斯顿被炸成一个窟窿城市。联军占领后,三一教堂广场边的一个咖啡馆外摆出几张椅子。可是,客人要预定,明天才有咖啡。后来,面包可以预定,午餐也行。人们开始习惯在此约会。在一片废墟中,老板积极的行动逐渐把咖啡馆变成周边英美盟军频繁光顾的社交中心。事例虽小,它体现行动建模的主要精神。
对于如何理解和运用小概率事件背后的厚数据,哈伯德(Douglas Hubbard)、马奇(James March)和维克(Karl Weick)等学者都给出有实践意义的建议。概括如下:
1.捕捉临界值,不做事后诸葛亮。例如,以色列对能威胁到中心城市的火炮力量异常敏感。一旦敌手掌握到接近临界值门槛的攻击力量,以方必定发动攻击,直至将对方实力压制到进攻门槛之下。
2.对无知新现象,建立“微积分”思维态度,不求完美,只求不断接近。古希腊人埃拉托色尼(Eratosthenes)发明一种方法,在两个不同地点,测量太阳正午时分正射和斜射的角度和两地距离,以此来计算地球周长。它是第一个地球周长值。尽管误差很大,它代表认识的一大跃进。
3.小数据为主,大数据为辅。1916年,德国人理查森(Lewis Fry Richardson)尝试把当地的气候情况(小数据)汇总在一起,做全国预测(大数据分析)。他的做法是把全国气候划分成纵横交错的格子矩阵。每个格子的气候情况对周边格子的影响可以简化处理。如此这般,他认为,即便是非常复杂的天气现象,也可以预测。理查森没有成功,因为计算力的限制。上世纪50年代,数学家纽曼利用大型计算机将这个方法运用到天气预报中。
4.运用“贝叶斯法则”(Bayes Theorem),为渐确定性创造前提条件。费米曾经问学生,芝加哥有多少钢琴调琴师?懂贝叶斯法则的学生给出估算公式:估算每一百个家庭有多少钢琴,钢琴与调琴师的比例,城市总人口,大约家庭数……贝叶斯概率思想的优势就是为不知道的现象创造可知的前提,然后逐渐确定。
5.收集临界危机事件,训练洞察能力。那些差一点就酿成大祸的临界危机是训练洞察力最好的案例,因为隐藏在深处的问题几乎都暴露出来了。比较2008年胶济铁路出轨事件和2011年甬温线重大事故,前一次已经暴露内部管理缺陷。它已经显示,组织内部周而复始的流程不能对付突然出现的变差。
6.运用想象力,对罕见事故做有故事情节的解释。丰富的解释可以依据不同利益相关者的立场,可以来自不同理论视角,可以结合感性和理性分析。想象力,特别是文学想象力,能够突破概念成见的束缚,照亮认识的盲点。例如,对疫情,我们可以从医学、传染病学、社会学、物流管理、心理学、国际政治的不同视角去理解。
7.在领域和区域属性很强的问题上,倾听专家判断。专家对一个细分领域中的知识脉络比较了解。我们看到的小概率事件,有时,他们拥有更多的历史样本。专家在纵向历史方面的积累可以弥补危机主事者单薄的知识。如图所示,对于动态变化的高频事件,如果特定领域或地域特征也极强,专家判断更可靠。上世纪90年代,根据旧金山地区同性恋肝炎发病率上升情况,数据分析人员预测艾滋病例也会相应增加。但长期深入社区的专家认为,同性恋社群已经接受艾滋病的现实,他们主动在社交媒体上说明自己的情况,以避免交叉感染。因此,病例不会上升。事实证明,了解当地情况的专家判断是正确的。
对于上面讨论的四种知识体系,我们如何选择?统计学家伯克斯(George E. Box)曾说:所有的模式都不完美,但有些更有用!没有一个特别的知识体系最适合小概率事件的危机。不过,有了这些不完美的模式,我们可以在实践中尝试,找到更有用的那一个。
实验室中有个经典玩笑:小白鼠说,我把实验员训练得超级听话,我一拉线,他就送实物。要避免成为小白鼠,我们就从掌握上面的知识体系分类开始。
(本篇为澎湃商学院独家专栏“危机不慌”系列之七,作者鲍勇剑为加拿大莱桥大学迪隆商学院终身教授、复旦大学管理学院EMBA项目特聘教授)
